Safe Reinforcement Learning with Instantaneous Constraints: The Role of Aggressive Exploration
Paper and Code
Dec 22, 2023

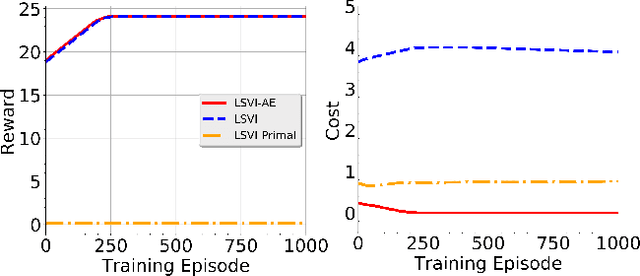
This paper studies safe Reinforcement Learning (safe RL) with linear function approximation and under hard instantaneous constraints where unsafe actions must be avoided at each step. Existing studies have considered safe RL with hard instantaneous constraints, but their approaches rely on several key assumptions: $(i)$ the RL agent knows a safe action set for {\it every} state or knows a {\it safe graph} in which all the state-action-state triples are safe, and $(ii)$ the constraint/cost functions are {\it linear}. In this paper, we consider safe RL with instantaneous hard constraints without assumption $(i)$ and generalize $(ii)$ to Reproducing Kernel Hilbert Space (RKHS). Our proposed algorithm, LSVI-AE, achieves $\tilde{\cO}(\sqrt{d^3H^4K})$ regret and $\tilde{\cO}(H \sqrt{dK})$ hard constraint violation when the cost function is linear and $\cO(H\gamma_K \sqrt{K})$ hard constraint violation when the cost function belongs to RKHS. Here $K$ is the learning horizon, $H$ is the length of each episode, and $\gamma_K$ is the information gain w.r.t the kernel used to approximate cost functions. Our results achieve the optimal dependency on the learning horizon $K$, matching the lower bound we provide in this paper and demonstrating the efficiency of LSVI-AE. Notably, the design of our approach encourages aggressive policy exploration, providing a unique perspective on safe RL with general cost functions and no prior knowledge of safe actions, which may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge