Safe Continuous Control with Constrained Model-Based Policy Optimization
Paper and Code
Apr 14, 2021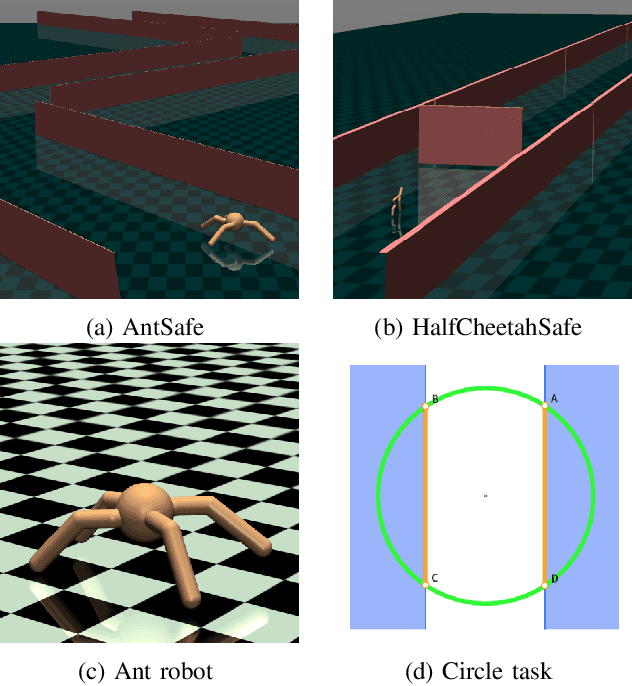
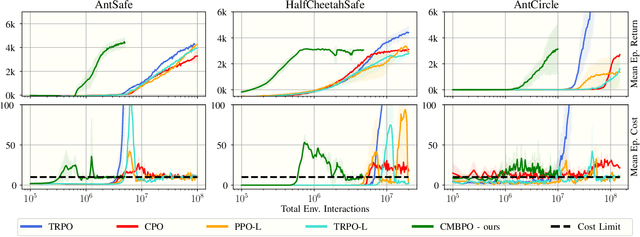
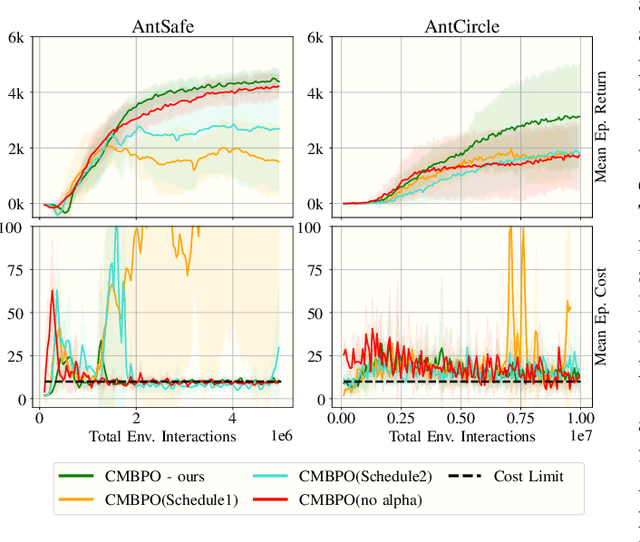

The applicability of reinforcement learning (RL) algorithms in real-world domains often requires adherence to safety constraints, a need difficult to address given the asymptotic nature of the classic RL optimization objective. In contrast to the traditional RL objective, safe exploration considers the maximization of expected returns under safety constraints expressed in expected cost returns. We introduce a model-based safe exploration algorithm for constrained high-dimensional control to address the often prohibitively high sample complexity of model-free safe exploration algorithms. Further, we provide theoretical and empirical analyses regarding the implications of model-usage on constrained policy optimization problems and introduce a practical algorithm that accelerates policy search with model-generated data. The need for accurate estimates of a policy's constraint satisfaction is in conflict with accumulating model-errors. We address this issue by quantifying model-uncertainty as the expected Kullback-Leibler divergence between predictions of an ensemble of probabilistic dynamics models and constrain this error-measure, resulting in an adaptive resampling scheme and dynamically limited rollout horizons. We evaluate this approach on several simulated constrained robot locomotion tasks with high-dimensional action- and state-spaces. Our empirical studies find that our algorithm reaches model-free performances with a 10-20 fold reduction of training samples while maintaining approximate constraint satisfaction levels of model-free methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge