Runaway Feedback Loops in Predictive Policing
Paper and Code
Dec 22, 2017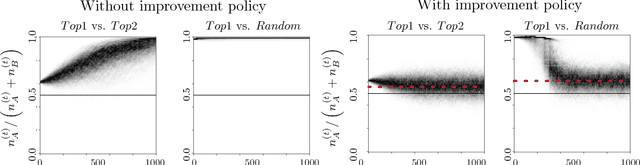
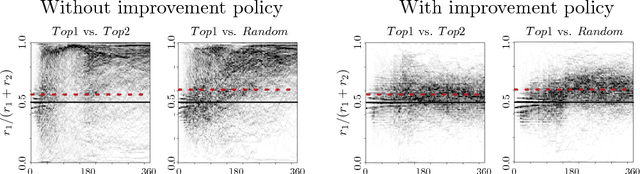
Predictive policing systems are increasingly used to determine how to allocate police across a city in order to best prevent crime. Discovered crime data (e.g., arrest counts) are used to help update the model, and the process is repeated. Such systems have been empirically shown to be susceptible to runaway feedback loops, where police are repeatedly sent back to the same neighborhoods regardless of the true crime rate. In response, we develop a mathematical model of predictive policing that proves why this feedback loop occurs, show empirically that this model exhibits such problems, and demonstrate how to change the inputs to a predictive policing system (in a black-box manner) so the runaway feedback loop does not occur, allowing the true crime rate to be learned. Our results are quantitative: we can establish a link (in our model) between the degree to which runaway feedback causes problems and the disparity in crime rates between areas. Moreover, we can also demonstrate the way in which \emph{reported} incidents of crime (those reported by residents) and \emph{discovered} incidents of crime (i.e. those directly observed by police officers dispatched as a result of the predictive policing algorithm) interact: in brief, while reported incidents can attenuate the degree of runaway feedback, they cannot entirely remove it without the interventions we suggest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge