RSA: Byzantine-Robust Stochastic Aggregation Methods for Distributed Learning from Heterogeneous Datasets
Paper and Code
Nov 09, 2018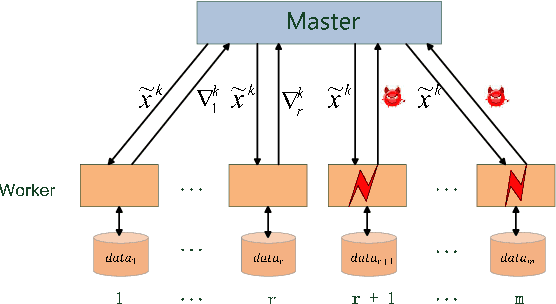
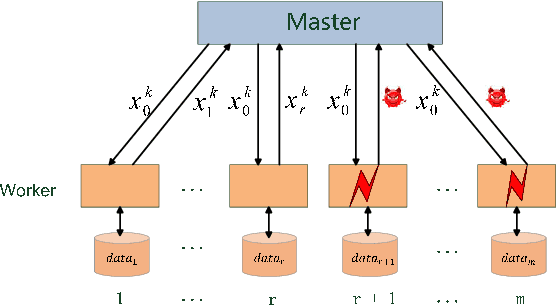
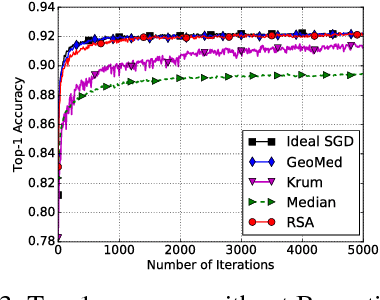
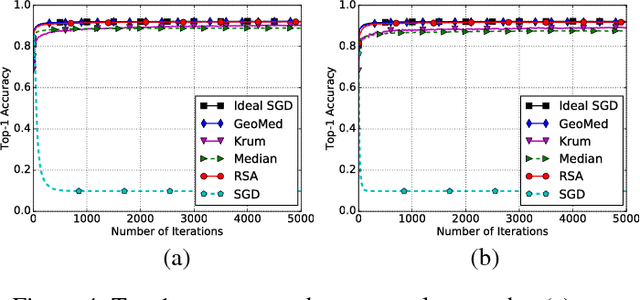
In this paper, we propose a class of robust stochastic subgradient methods for distributed learning from heterogeneous datasets at presence of an unknown number of Byzantine workers. The Byzantine workers, during the learning process, may send arbitrary incorrect messages to the master due to data corruptions, communication failures or malicious attacks, and consequently bias the learned model. The key to the proposed methods is a regularization term incorporated with the objective function so as to robustify the learning task and mitigate the negative effects of Byzantine attacks. The resultant subgradient-based algorithms are termed Byzantine-Robust Stochastic Aggregation methods, justifying our acronym RSA used henceforth. In contrast to most of the existing algorithms, RSA does not rely on the assumption that the data are independent and identically distributed (i.i.d.) on the workers, and hence fits for a wider class of applications. Theoretically, we show that: i) RSA converges to a near-optimal solution with the learning error dependent on the number of Byzantine workers; ii) the convergence rate of RSA under Byzantine attacks is the same as that of the stochastic gradient descent method, which is free of Byzantine attacks. Numerically, experiments on real dataset corroborate the competitive performance of RSA and a complexity reduction compared to the state-of-the-art alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge