RRT-CoLearn: towards kinodynamic planning without numerical trajectory optimization
Paper and Code
Oct 27, 2017
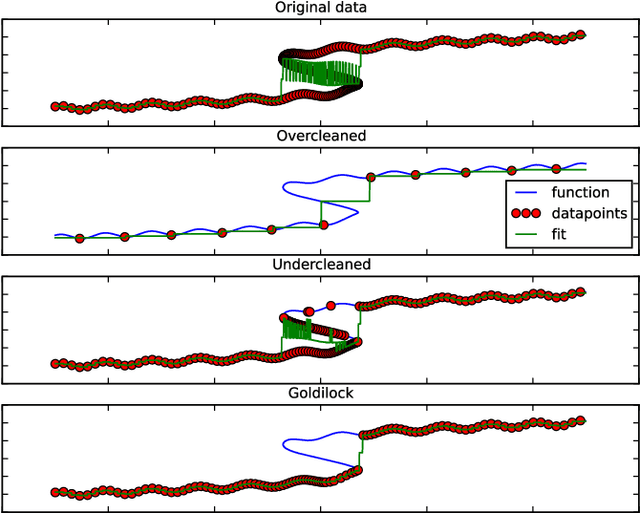
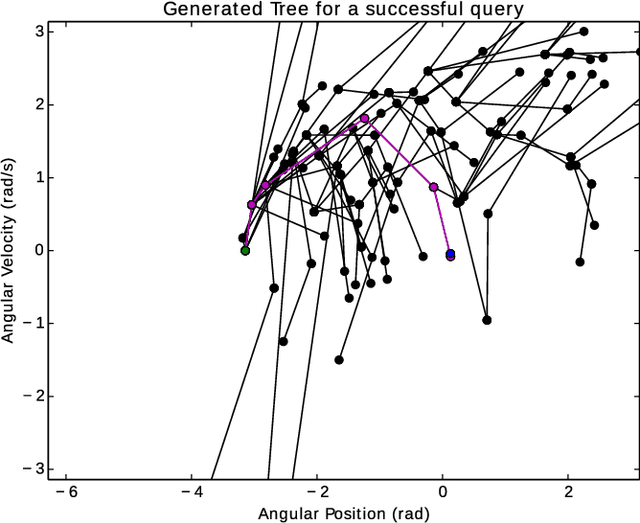
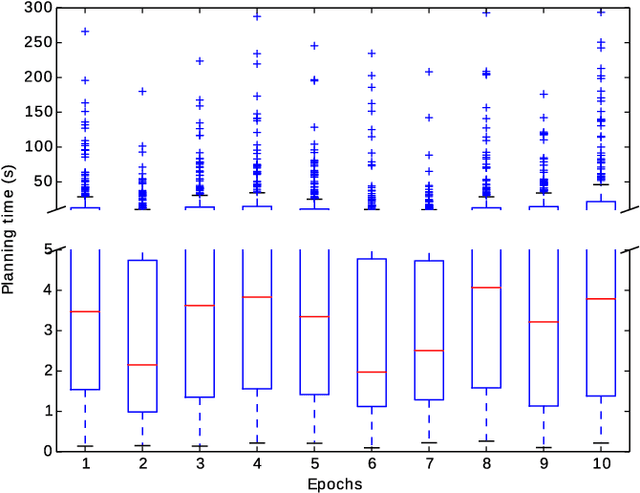
Sampling-based kinodynamic planners, such as Rapidly-exploring Random Trees (RRTs), pose two fundamental challenges: computing a reliable (pseudo-)metric for the distance between two randomly sampled nodes, and computing a steering input to connect the nodes. The core of these challenges is a Two Point Boundary Value Problem, which is known to be NP-hard. Recently, the distance metric has been approximated using supervised learning, reducing computation time drastically. The previous work on such learning RRTs use direct optimal control to generate the data for supervised learning. This paper proposes to use indirect optimal control instead, because it provides two benefits: it reduces the computational effort to generate the data, and it provides a low dimensional parametrization of the action space. The latter allows us to learn both the distance metric and the steering input to connect two nodes. This eliminates the need for a local planner in learning RRTs. Experimental results on a pendulum swing up show 10-fold speed-up in both the offline data generation and the online planning time, leading to at least a 10-fold speed-up in the overall planning time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge