Rotational Diversity in Multi-Cycle Assignment Problems

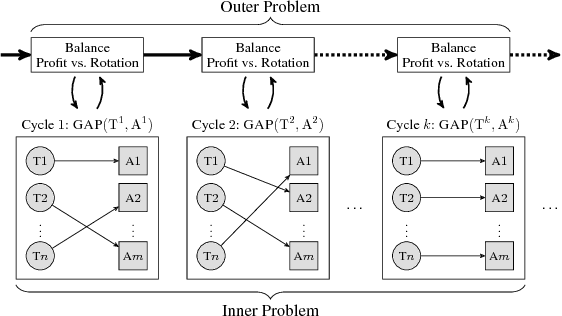
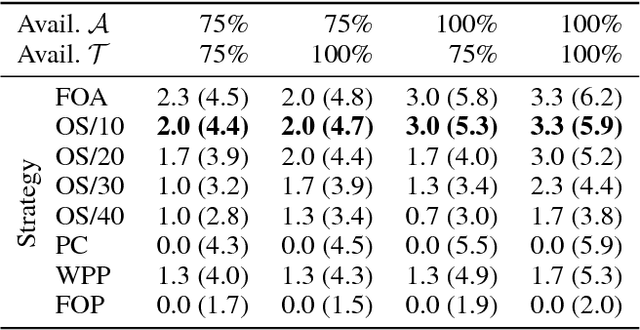
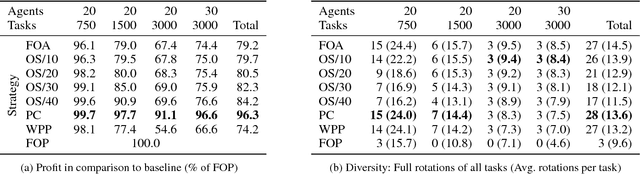
In multi-cycle assignment problems with rotational diversity, a set of tasks has to be repeatedly assigned to a set of agents. Over multiple cycles, the goal is to achieve a high diversity of assignments from tasks to agents. At the same time, the assignments' profit has to be maximized in each cycle. Due to changing availability of tasks and agents, planning ahead is infeasible and each cycle is an independent assignment problem but influenced by previous choices. We approach the multi-cycle assignment problem as a two-part problem: Profit maximization and rotation are combined into one objective value, and then solved as a General Assignment Problem. Rotational diversity is maintained with a single execution of the costly assignment model. Our simple, yet effective method is applicable to different domains and applications. Experiments show the applicability on a multi-cycle variant of the multiple knapsack problem and a real-world case study on the test case selection and assignment problem, an example from the software engineering domain, where test cases have to be distributed over compatible test machines.