Robust subgroup discovery
Paper and Code
Mar 25, 2021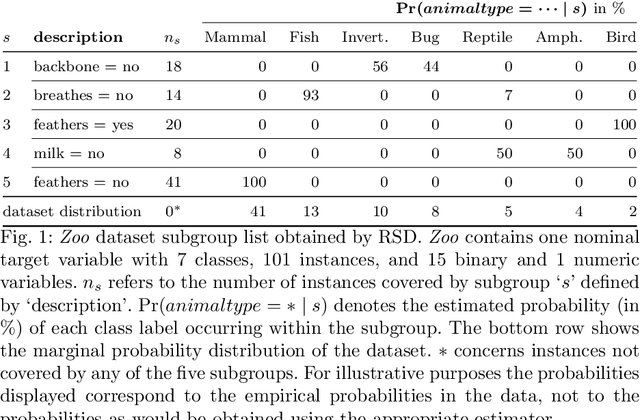
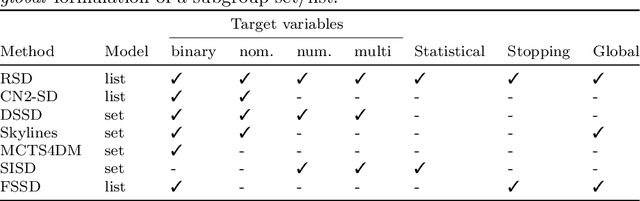


We introduce the problem of robust subgroup discovery, i.e., finding a set of interpretable descriptions of subsets that 1) stand out with respect to one or more target attributes, 2) are statistically robust, and 3) non-redundant. Many attempts have been made to mine either locally robust subgroups or to tackle the pattern explosion, but we are the first to address both challenges at the same time from a global perspective. First, we formulate a broad model class of subgroup lists, i.e., ordered sets of subgroups, for univariate and multivariate targets that can consist of nominal or numeric variables. This novel model class allows us to formalize the problem of optimal robust subgroup discovery using the Minimum Description Length (MDL) principle, where we resort to optimal Normalized Maximum Likelihood and Bayesian encodings for nominal and numeric targets, respectively. Notably, we show that our problem definition is equal to mining the top-1 subgroup with an information-theoretic quality measure plus a penalty for complexity. Second, as finding optimal subgroup lists is NP-hard, we propose RSD, a greedy heuristic that finds good subgroup lists and guarantees that the most significant subgroup found according to the MDL criterion is added in each iteration, which is shown to be equivalent to a Bayesian one-sample proportions, multinomial, or t-test between the subgroup and dataset marginal target distributions plus a multiple hypothesis testing penalty. We empirically show on 54 datasets that RSD outperforms previous subgroup set discovery methods in terms of quality and subgroup list size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge