Robust partial Fourier reconstruction for diffusion-weighted imaging using a recurrent convolutional neural network

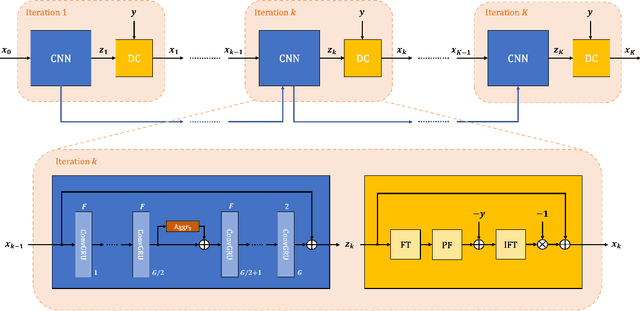
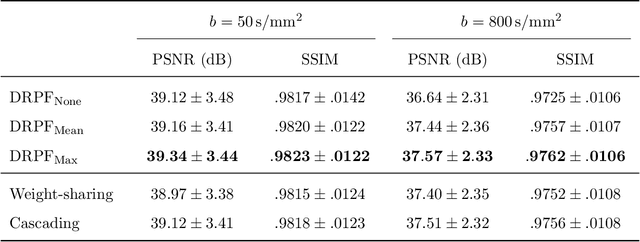
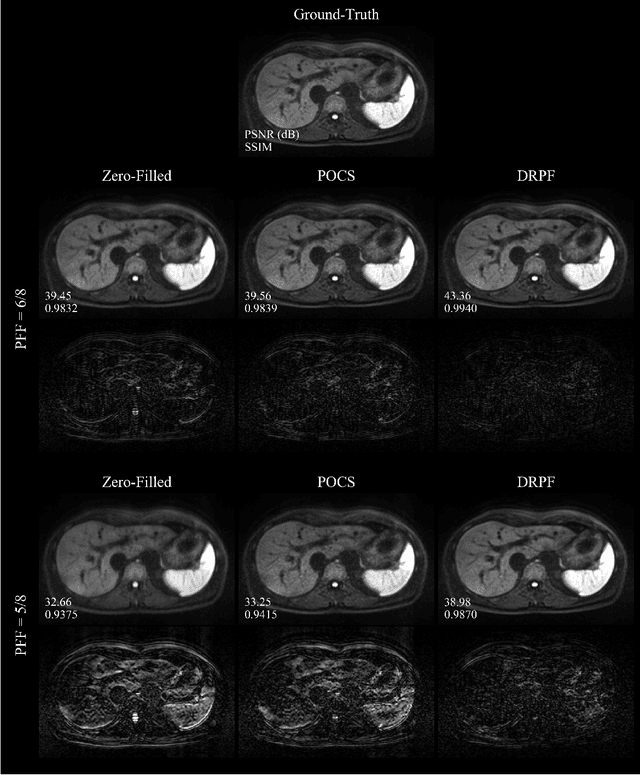
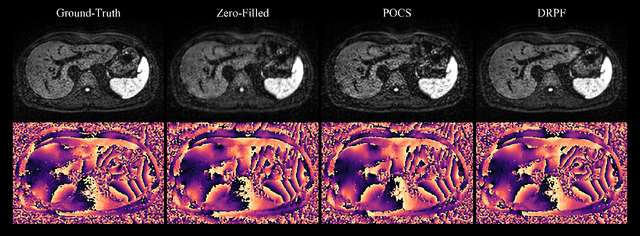
Purpose: To develop an algorithm for robust partial Fourier (PF) reconstruction applicable to diffusion-weighted (DW) images with non-smooth phase variations. Methods: Based on an unrolled proximal splitting algorithm, a neural network architecture is derived which alternates between data consistency operations and regularization implemented by recurrent convolutions. In order to exploit correlations, multiple repetitions of the same slice are jointly reconstructed under consideration of permutation-equivariance. The proposed method is trained on DW liver data of 60 volunteers and evaluated on retrospectively and prospectively sub-sampled data of different anatomies and resolutions. In addition, the benefits of using a recurrent network over other unrolling strategies is investigated. Results: Conventional PF techniques can be significantly outperformed in terms of quantitative measures as well as perceptual image quality. The proposed method is able to generalize well to brain data with contrasts and resolution not present in the training set. The reduction in echo time (TE) associated with prospective PF-sampling enables DW imaging with higher signal. Also, the TE increase in acquisitions with higher resolution can be compensated for. It can be shown that unrolling by means of a recurrent network produced better results than using a weight-shared network or a cascade of networks. Conclusion: This work demonstrates that robust PF reconstruction of DW data is feasible even at strong PF factors in applications with severe phase variations. Since the proposed method does not rely on smoothness priors of the phase but uses learned recurrent convolutions instead, artifacts of conventional PF methods can be avoided.