Robust normalizing flows using Bernstein-type polynomials

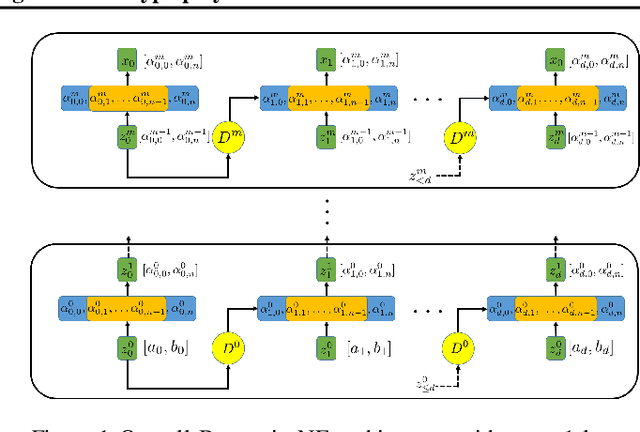
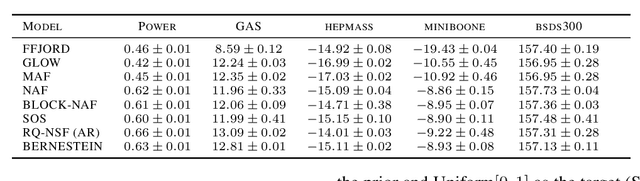
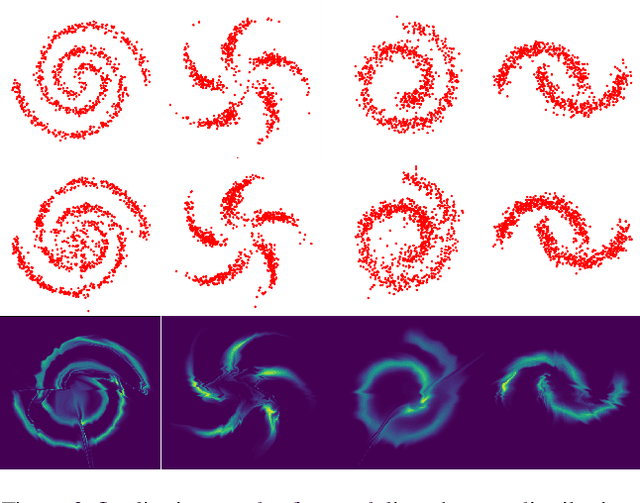
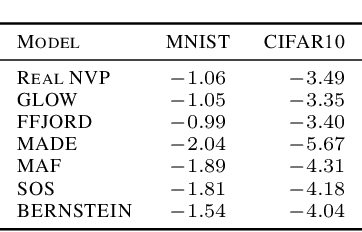
Normalizing flows (NFs) are a class of generative models that allows exact density evaluation and sampling. We propose a framework to construct NFs based on increasing triangular maps and Bernstein-type polynomials. Compared to the existing (universal) NF frameworks, our method provides compelling advantages like theoretical upper bounds for the approximation error, robustness, higher interpretability, suitability for compactly supported densities, and the ability to employ higher degree polynomials without training instability. Moreover, we provide a constructive universality proof, which gives analytic expressions of the approximations for known transformations. We conduct a thorough theoretical analysis and empirically demonstrate the efficacy of the proposed technique using experiments on both real-world and synthetic datasets.