Robust Kernelized Multi-View Self-Representations for Clustering by Tensor Multi-Rank Minimization
Paper and Code
Sep 15, 2017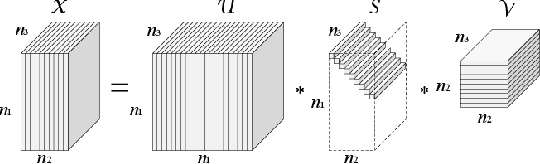

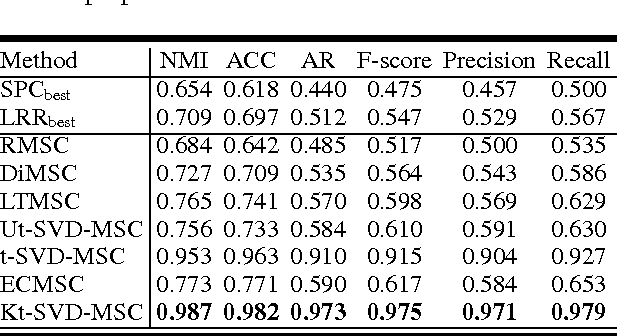
Most recently, tensor-SVD is implemented on multi-view self-representation clustering and has achieved the promising results in many real-world applications such as face clustering, scene clustering and generic object clustering. However, tensor-SVD based multi-view self-representation clustering is proposed originally to solve the clustering problem in the multiple linear subspaces, leading to unsatisfactory results when dealing with the case of non-linear subspaces. To handle data clustering from the non-linear subspaces, a kernelization method is designed by mapping the data from the original input space to a new feature space in which the transformed data can be clustered by a multiple linear clustering method. In this paper, we make an optimization model for the kernelized multi-view self-representation clustering problem. We also develop a new efficient algorithm based on the alternation direction method and infer a closed-form solution. Since all the subproblems can be solved exactly, the proposed optimization algorithm is guaranteed to obtain the optimal solution. In particular, the original tensor-based multi-view self-representation clustering problem is a special case of our approach and can be solved by our algorithm. Experimental results on several popular real-world clustering datasets demonstrate that our approach achieves the state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge