Robust factored principal component analysis for matrix-valued outlier accommodation and detection
Paper and Code
Dec 13, 2021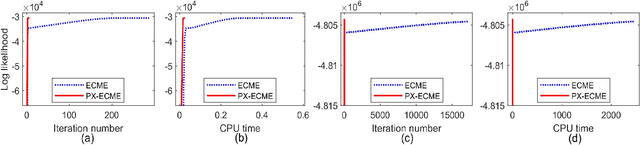
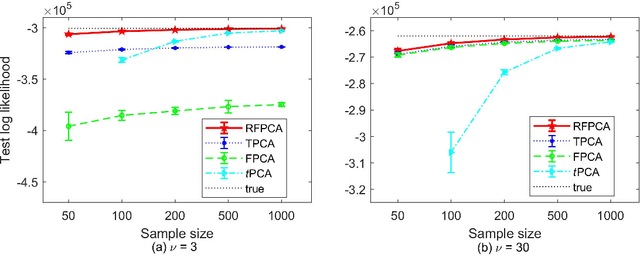
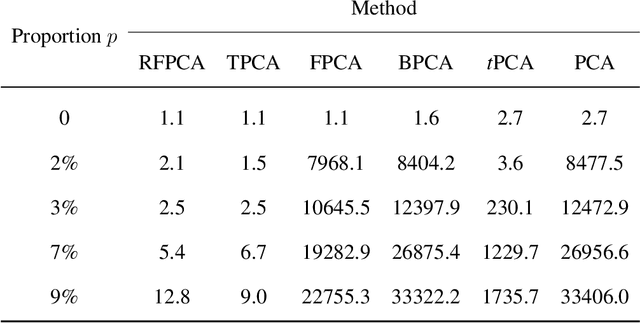
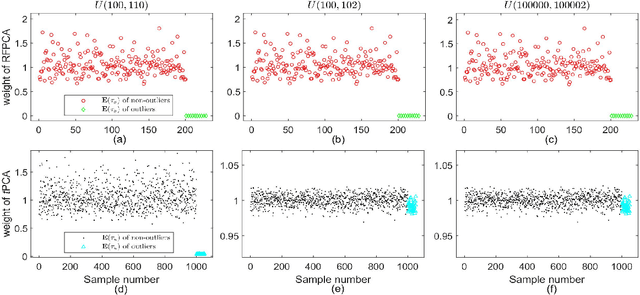
Principal component analysis (PCA) is a popular dimension reduction technique for vector data. Factored PCA (FPCA) is a probabilistic extension of PCA for matrix data, which can substantially reduce the number of parameters in PCA while yield satisfactory performance. However, FPCA is based on the Gaussian assumption and thereby susceptible to outliers. Although the multivariate $t$ distribution as a robust modeling tool for vector data has a very long history, its application to matrix data is very limited. The main reason is that the dimension of the vectorized matrix data is often very high and the higher the dimension, the lower the breakdown point that measures the robustness. To solve the robustness problem suffered by FPCA and make it applicable to matrix data, in this paper we propose a robust extension of FPCA (RFPCA), which is built upon a $t$-type distribution called matrix-variate $t$ distribution. Like the multivariate $t$ distribution, the matrix-variate $t$ distribution can adaptively down-weight outliers and yield robust estimates. We develop a fast EM-type algorithm for parameter estimation. Experiments on synthetic and real-world datasets reveal that RFPCA is compared favorably with several related methods and RFPCA is a simple but powerful tool for matrix-valued outlier detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge