Robust Counterfactual Explanations for Random Forests

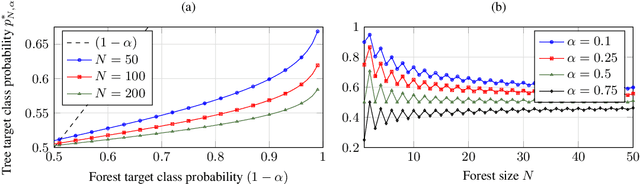
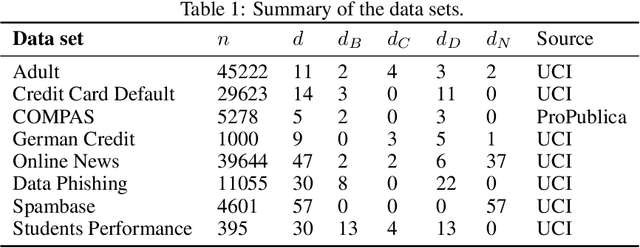
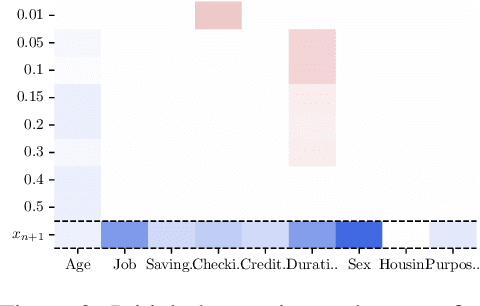
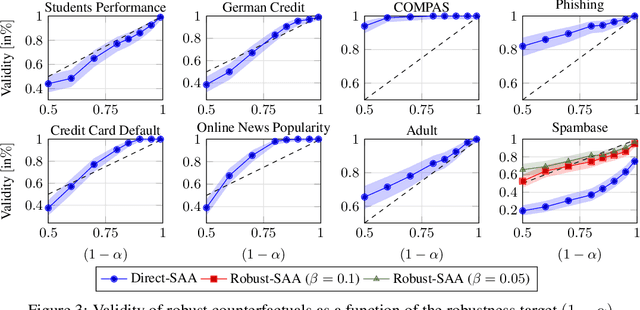
Counterfactual explanations describe how to modify a feature vector in order to flip the outcome of a trained classifier. Several heuristic and optimal methods have been proposed to generate these explanations. However, the robustness of counterfactual explanations when the classifier is re-trained has yet to be studied. Our goal is to obtain counterfactual explanations for random forests that are robust to algorithmic uncertainty. We study the link between the robustness of ensemble models and the robustness of base learners and frame the generation of robust counterfactual explanations as a chance-constrained optimization problem. We develop a practical method with good empirical performance and provide finite-sample and asymptotic guarantees for simple random forests of stumps. We show that existing methods give surprisingly low robustness: the validity of naive counterfactuals is below $50\%$ on most data sets and can fall to $20\%$ on large problem instances with many features. Even with high plausibility, counterfactual explanations often exhibit low robustness to algorithmic uncertainty. In contrast, our method achieves high robustness with only a small increase in the distance from counterfactual explanations to their initial observations. Furthermore, we highlight the connection between the robustness of counterfactual explanations and the predictive importance of features.