Risk-Aware Submodular Optimization for Multi-objective Travelling Salesperson Problem
Paper and Code
Nov 02, 2020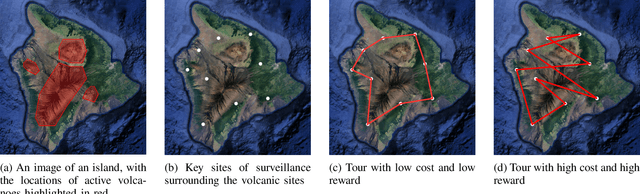
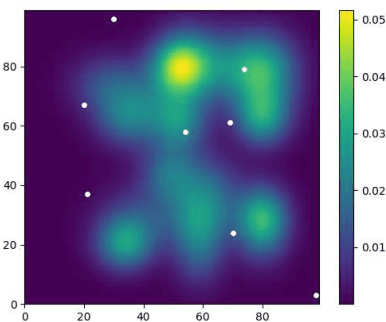
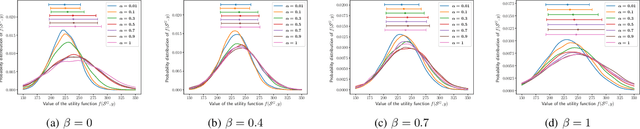
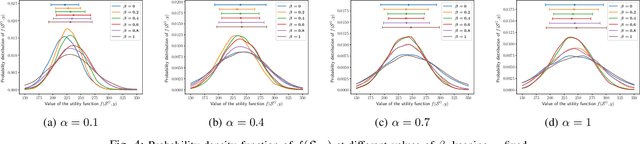
We introduce a risk-aware multi-objective Traveling Salesperson Problem (TSP) variant, where the robot tour cost and tour reward have to be optimized simultaneously. The robot obtains reward along the edges in the graph. We study the case where the rewards and the costs exhibit diminishing marginal gains, i.e., are submodular. Unlike prior work, we focus on the scenario where the costs and the rewards are uncertain and seek to maximize the Conditional-Value-at-Risk (CVaR) metric of the submodular function. We propose a risk-aware greedy algorithm (RAGA) to find a bounded-approximation algorithm. The approximation algorithm runs in polynomial time and is within a constant factor of the optimal and an additive term that depends on the optimal solution. We use the submodular function's curvature to improve approximation results further and verify the algorithm's performance through simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge