RIM-Net: Recursive Implicit Fields for Unsupervised Learning of Hierarchical Shape Structures
Paper and Code
Jan 30, 2022


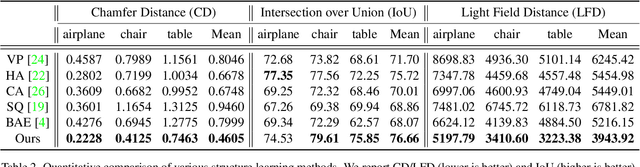
We introduce RIM-Net, a neural network which learns recursive implicit fields for unsupervised inference of hierarchical shape structures. Our network recursively decomposes an input 3D shape into two parts, resulting in a binary tree hierarchy. Each level of the tree corresponds to an assembly of shape parts, represented as implicit functions, to reconstruct the input shape. At each node of the tree, simultaneous feature decoding and shape decomposition are carried out by their respective feature and part decoders, with weight sharing across the same hierarchy level. As an implicit field decoder, the part decoder is designed to decompose a sub-shape, via a two-way branched reconstruction, where each branch predicts a set of parameters defining a Gaussian to serve as a local point distribution for shape reconstruction. With reconstruction losses accounted for at each hierarchy level and a decomposition loss at each node, our network training does not require any ground-truth segmentations, let alone hierarchies. Through extensive experiments and comparisons to state-of-the-art alternatives, we demonstrate the quality, consistency, and interpretability of hierarchical structural inference by RIM-Net.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge