RFM-SLAM: Exploiting Relative Feature Measurements to Separate Orientation and Position Estimation in SLAM
Paper and Code
Sep 16, 2016
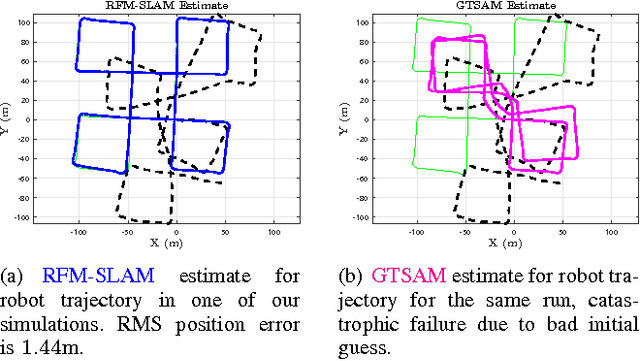
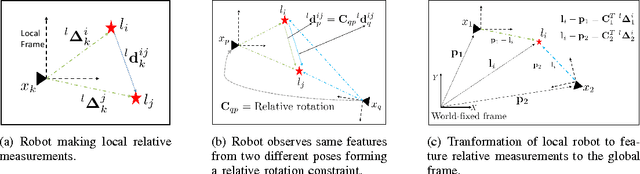

The SLAM problem is known to have a special property that when robot orientation is known, estimating the history of robot poses and feature locations can be posed as a standard linear least squares problem. In this work, we develop a SLAM framework that uses relative feature-to-feature measurements to exploit this structural property of SLAM. Relative feature measurements are used to pose a linear estimation problem for pose-to-pose orientation constraints. This is followed by solving an iterative non-linear on-manifold optimization problem to compute the maximum likelihood estimate for robot orientation given relative rotation constraints. Once the robot orientation is computed, we solve a linear problem for robot position and map estimation. Our approach reduces the computational burden of non-linear optimization by posing a smaller optimization problem as compared to standard graph-based methods for feature-based SLAM. Further, empirical results show our method avoids catastrophic failures that arise in existing methods due to using odometery as an initial guess for non-linear optimization, while its accuracy degrades gracefully as sensor noise is increased. We demonstrate our method through extensive simulations and comparisons with an existing state-of-the-art solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge