Reward-Based Collision-Free Algorithm for Trajectory Planning of Autonomous Robots
Paper and Code
Feb 10, 2025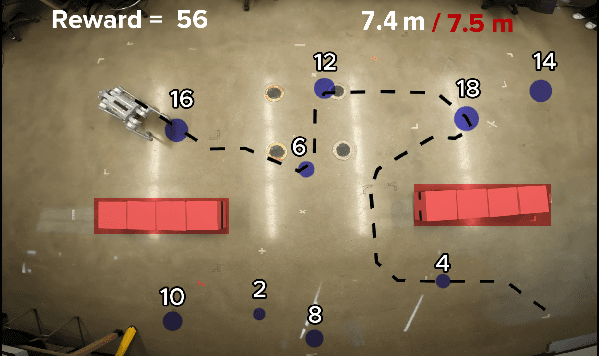
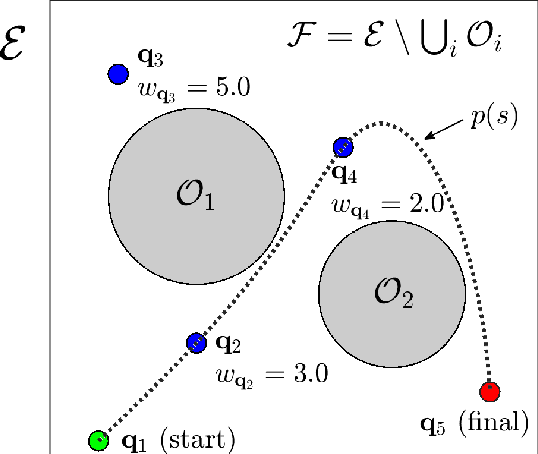
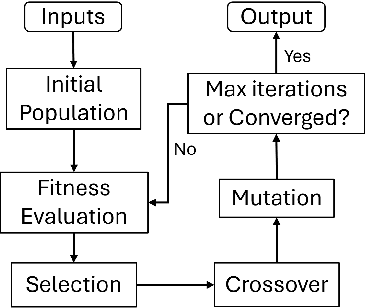
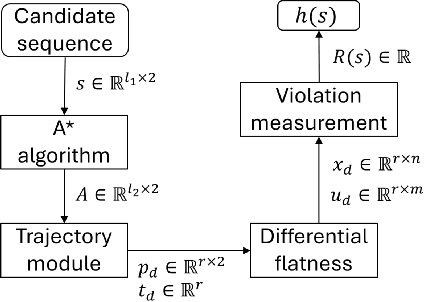
This paper introduces a new mission planning algorithm for autonomous robots that enables the reward-based selection of an optimal waypoint sequence from a predefined set. The algorithm computes a feasible trajectory and corresponding control inputs for a robot to navigate between waypoints while avoiding obstacles, maximizing the total reward, and adhering to constraints on state, input and its derivatives, mission time window, and maximum distance. This also solves a generalized prize-collecting traveling salesman problem. The proposed algorithm employs a new genetic algorithm that evolves solution candidates toward the optimal solution based on a fitness function and crossover. During fitness evaluation, a penalty method enforces constraints, and the differential flatness property with clothoid curves efficiently penalizes infeasible trajectories. The Euler spiral method showed promising results for trajectory parameterization compared to minimum snap and jerk polynomials. Due to the discrete exploration space, crossover is performed using a dynamic time-warping-based method and extended convex combination with projection. A mutation step enhances exploration. Results demonstrate the algorithm's ability to find the optimal waypoint sequence, fulfill constraints, avoid infeasible waypoints, and prioritize high-reward ones. Simulations and experiments with a ground vehicle, quadrotor, and quadruped are presented, complemented by benchmarking and a time-complexity analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge