Revisiting State Augmentation methods for Reinforcement Learning with Stochastic Delays
Paper and Code
Aug 17, 2021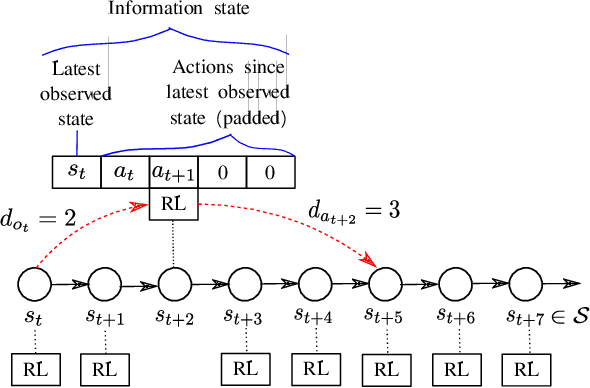
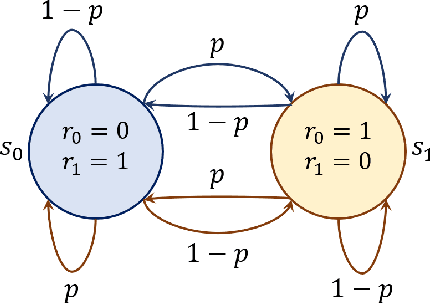
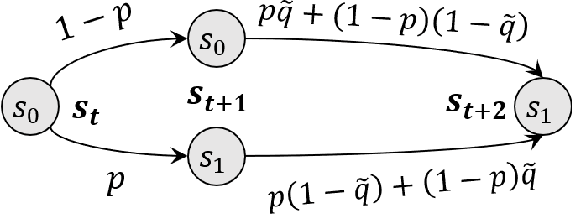
Several real-world scenarios, such as remote control and sensing, are comprised of action and observation delays. The presence of delays degrades the performance of reinforcement learning (RL) algorithms, often to such an extent that algorithms fail to learn anything substantial. This paper formally describes the notion of Markov Decision Processes (MDPs) with stochastic delays and shows that delayed MDPs can be transformed into equivalent standard MDPs (without delays) with significantly simplified cost structure. We employ this equivalence to derive a model-free Delay-Resolved RL framework and show that even a simple RL algorithm built upon this framework achieves near-optimal rewards in environments with stochastic delays in actions and observations. The delay-resolved deep Q-network (DRDQN) algorithm is bench-marked on a variety of environments comprising of multi-step and stochastic delays and results in better performance, both in terms of achieving near-optimal rewards and minimizing the computational overhead thereof, with respect to the currently established algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge