Revisiting "Over-smoothing" in Deep GCNs

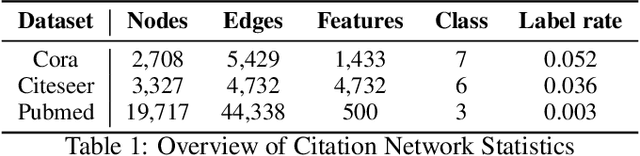
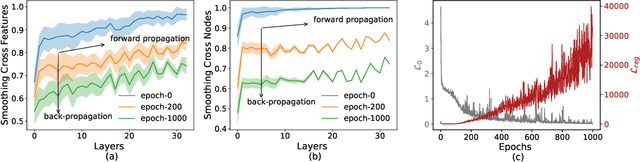
Oversmoothing has been assumed to be the major cause of performance drop in deep graph convolutional networks (GCNs). The evidence is usually derived from Simple Graph Convolution (SGC), a linear variant of GCNs. In this paper, we revisit graph node classification from an optimization perspective and argue that GCNs can actually learn anti-oversmoothing, whereas overfitting is the real obstacle in deep GCNs. This work interprets GCNs and SGCs as two-step optimization problems and provides the reason why deep SGC suffers from oversmoothing but deep GCNs do not. Our conclusion is compatible with the previous understanding of SGC, but we clarify why the same reasoning does not apply to GCNs. Based on our formulation, we provide more insights into the convolution operator and further propose a mean-subtraction trick to accelerate the training of deep GCNs. We verify our theory and propositions on three graph benchmarks. The experiments show that (i) in GCN, overfitting leads to the performance drop and oversmoothing does not exist even model goes to very deep (100 layers); (ii) mean-subtraction speeds up the model convergence as well as retains the same expressive power; (iii) the weight of neighbor averaging (1 is the common setting) does not significantly affect the model performance once it is above the threshold (> 0.5).