Revisiting Modified Greedy Algorithm for Monotone Submodular Maximization with a Knapsack Constraint
Paper and Code
Aug 12, 2020

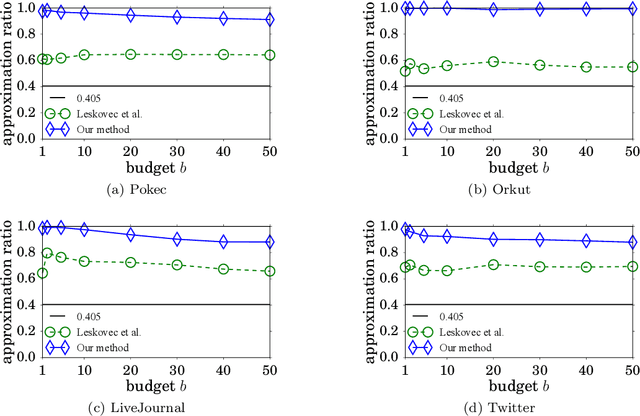
Monotone submodular maximization with a knapsack constraint is NP-hard. Various approximation algorithms have been devised to address this optimization problem. In this paper, we revisit the widely known modified greedy algorithm. First, we show that this algorithm can achieve an approximation factor of $0.405$, which significantly improves the known factor of $0.357$ given by Wolsey or $(1-1/\mathrm{e})/2\approx 0.316$ given by Khuller et al. More importantly, our analysis uncovers a gap in Khuller et al.'s proof for the extensively mentioned approximation factor of $(1-1/\sqrt{\mathrm{e}})\approx 0.393$ in the literature to clarify a long time of misunderstanding on this issue. Second, we enhance the modified greedy algorithm to derive a data-dependent upper bound on the optimum. We empirically demonstrate the tightness of our upper bound with a real-world application. The bound enables us to obtain a data-dependent ratio typically much higher than $0.405$ between the solution value of the modified greedy algorithm and the optimum. It can also be used to significantly improve the efficiency of algorithms such as branch and bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge