Revisiting Maximum Entropy Inverse Reinforcement Learning: New Perspectives and Algorithms
Paper and Code
Dec 01, 2020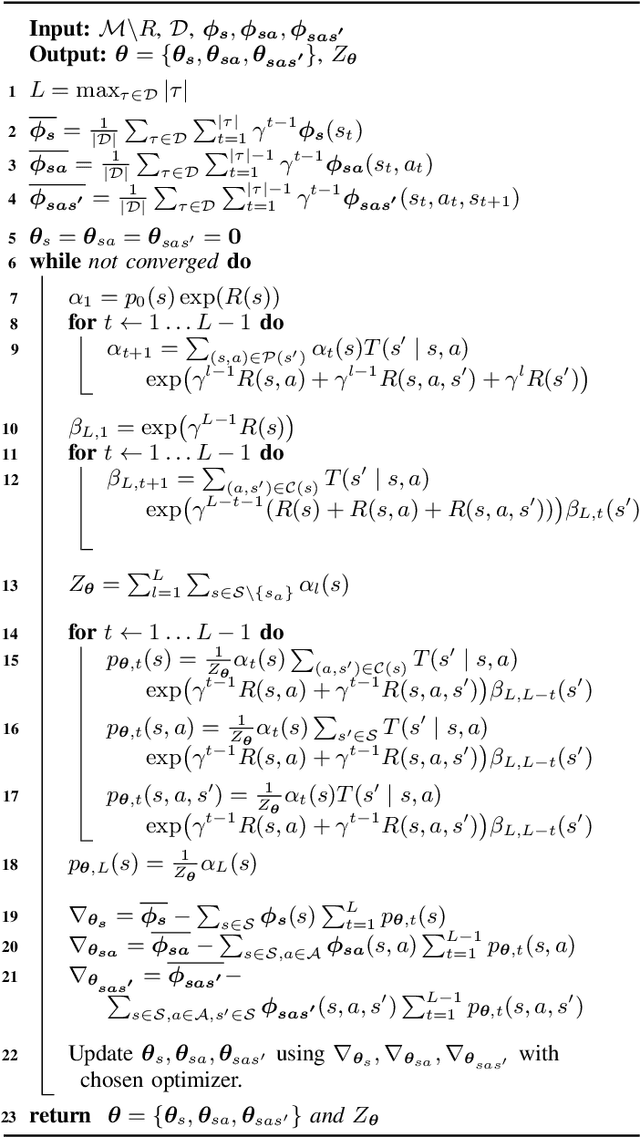
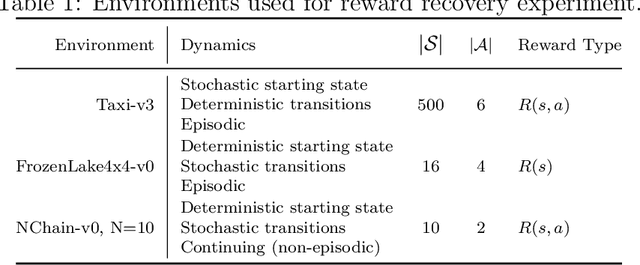
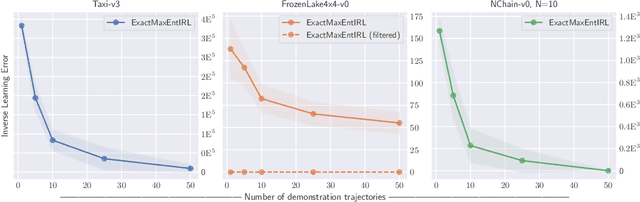
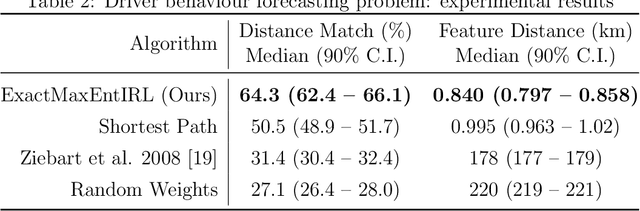
We provide new perspectives and inference algorithms for Maximum Entropy (MaxEnt) Inverse Reinforcement Learning (IRL), which provides a principled method to find a most non-committal reward function consistent with given expert demonstrations, among many consistent reward functions. We first present a generalized MaxEnt formulation based on minimizing a KL-divergence instead of maximizing an entropy. This improves the previous heuristic derivation of the MaxEnt IRL model (for stochastic MDPs), allows a unified view of MaxEnt IRL and Relative Entropy IRL, and leads to a model-free learning algorithm for the MaxEnt IRL model. Second, a careful review of existing inference algorithms and implementations showed that they approximately compute the marginals required for learning the model. We provide examples to illustrate this, and present an efficient and exact inference algorithm. Our algorithm can handle variable length demonstrations; in addition, while a basic version takes time quadratic in the maximum demonstration length L, an improved version of this algorithm reduces this to linear using a padding trick. Experiments show that our exact algorithm improves reward learning as compared to the approximate ones. Furthermore, our algorithm scales up to a large, real-world dataset involving driver behaviour forecasting. We provide an optimized implementation compatible with the OpenAI Gym interface. Our new insight and algorithms could possibly lead to further interest and exploration of the original MaxEnt IRL model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge