Revisiting Graph Convolutional Network on Semi-Supervised Node Classification from an Optimization Perspective
Paper and Code
Sep 25, 2020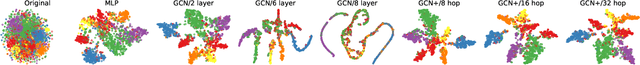
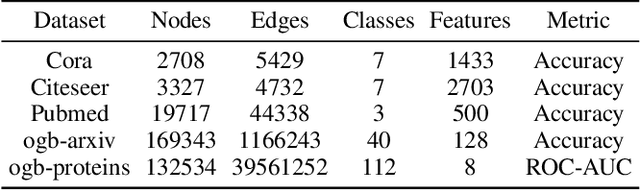
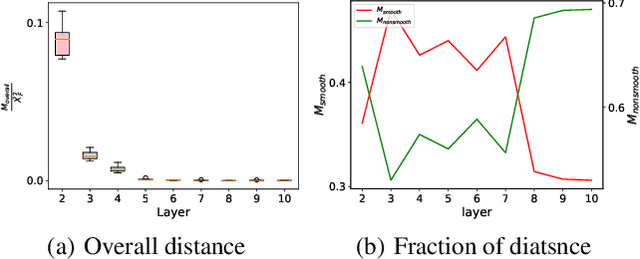
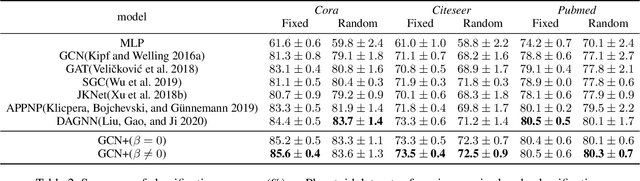
Graph convolutional networks (GCNs) have achieved promising performance on various graph-based tasks. However they suffer from over-smoothing when stacking more layers. In this paper, we present a quantitative study on this observation and develop novel insights towards the deeper GCN. First, we interpret the current graph convolutional operations from an optimization perspective and argue that over-smoothing is mainly caused by the naive first-order approximation of the solution to the optimization problem. Subsequently, we introduce two metrics to measure the over-smoothing on node-level tasks. Specifically, we calculate the fraction of the pairwise distance between connected and disconnected nodes to the overall distance respectively. Based on our theoretical and empirical analysis, we establish a universal theoretical framework of GCN from an optimization perspective and derive a novel convolutional kernel named GCN+ which has lower parameter amount while relieving the over-smoothing inherently. Extensive experiments on real-world datasets demonstrate the superior performance of GCN+ over state-of-the-art baseline methods on the node classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge