Revisiting 2D Convolutional Neural Networks for Graph-based Applications
Paper and Code
May 23, 2021
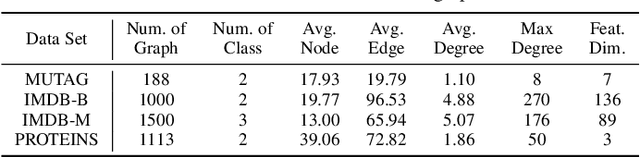
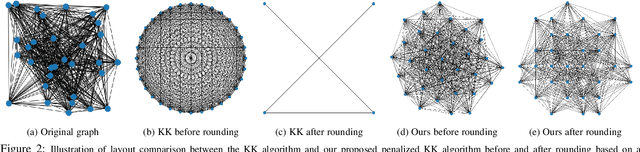
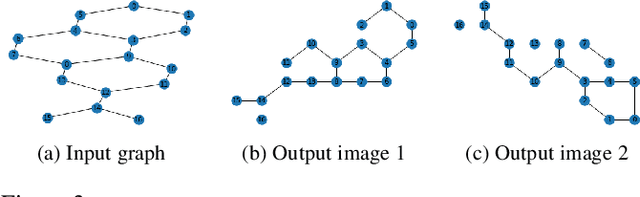
Graph convolutional networks (GCNs) are widely used in graph-based applications such as graph classification and segmentation. However, current GCNs have limitations on implementation such as network architectures due to their irregular inputs. In contrast, convolutional neural networks (CNNs) are capable of extracting rich features from large-scale input data, but they do not support general graph inputs. To bridge the gap between GCNs and CNNs, in this paper we study the problem of how to effectively and efficiently map general graphs to 2D grids that CNNs can be directly applied to, while preserving graph topology as much as possible. We therefore propose two novel graph-to-grid mapping schemes, namely, {\em graph-preserving grid layout (GPGL)} and its extension {\em Hierarchical GPGL (H-GPGL)} for computational efficiency. We formulate the GPGL problem as integer programming and further propose an approximate yet efficient solver based on a penalized Kamada-Kawai method, a well-known optimization algorithm in 2D graph drawing. We propose a novel vertex separation penalty that encourages graph vertices to lay on the grid without any overlap. Along with this image representation, even extra 2D maxpooling layers contribute to the PointNet, a widely applied point-based neural network. We demonstrate the empirical success of GPGL on general graph classification with small graphs and H-GPGL on 3D point cloud segmentation with large graphs, based on 2D CNNs including VGG16, ResNet50 and multi-scale maxout (MSM) CNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge