Rethinking Neural vs. Matrix-Factorization Collaborative Filtering: the Theoretical Perspectives
Paper and Code
Oct 23, 2021
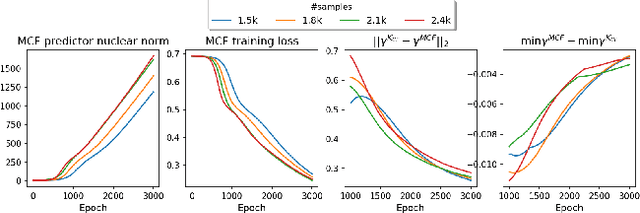

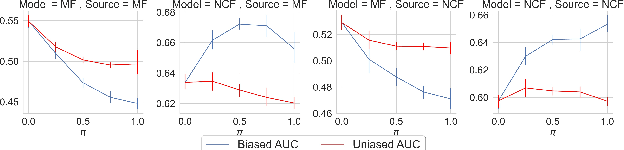
The recent work by Rendle et al. (2020), based on empirical observations, argues that matrix-factorization collaborative filtering (MCF) compares favorably to neural collaborative filtering (NCF), and conjectures the dot product's superiority over the feed-forward neural network as similarity function. In this paper, we address the comparison rigorously by answering the following questions: 1. what is the limiting expressivity of each model; 2. under the practical gradient descent, to which solution does each optimization path converge; 3. how would the models generalize under the inductive and transductive learning setting. Our results highlight the similar expressivity for the overparameterized NCF and MCF as kernelized predictors, and reveal the relation between their optimization paths. We further show their different generalization behaviors, where MCF and NCF experience specific tradeoff and comparison in the transductive and inductive collaborative filtering setting. Lastly, by showing a novel generalization result, we reveal the critical role of correcting exposure bias for model evaluation in the inductive setting. Our results explain some of the previously observed conflicts, and we provide synthetic and real-data experiments to shed further insights to this topic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge