Rethinking Fano's Inequality in Ensemble Learning

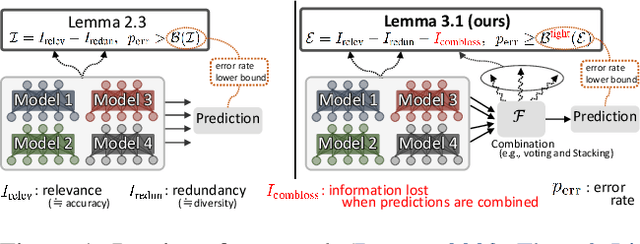
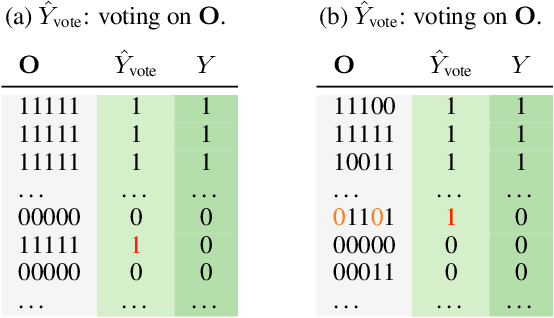
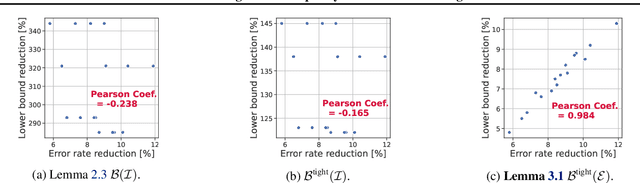
We propose a fundamental theory on ensemble learning that evaluates a given ensemble system by a well-grounded set of metrics. Previous studies used a variant of Fano's inequality of information theory and derived a lower bound of the classification error rate on the basis of the accuracy and diversity of models. We revisit the original Fano's inequality and argue that the studies did not take into account the information lost when multiple model predictions are combined into a final prediction. To address this issue, we generalize the previous theory to incorporate the information loss. Further, we empirically validate and demonstrate the proposed theory through extensive experiments on actual systems. The theory reveals the strengths and weaknesses of systems on each metric, which will push the theoretical understanding of ensemble learning and give us insights into designing systems.