Rethinking Bayesian Learning for Data Analysis: The Art of Prior and Inference in Sparsity-Aware Modeling
Paper and Code
May 28, 2022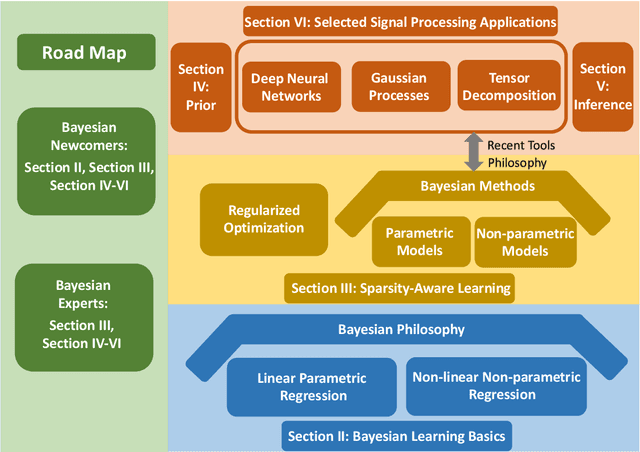
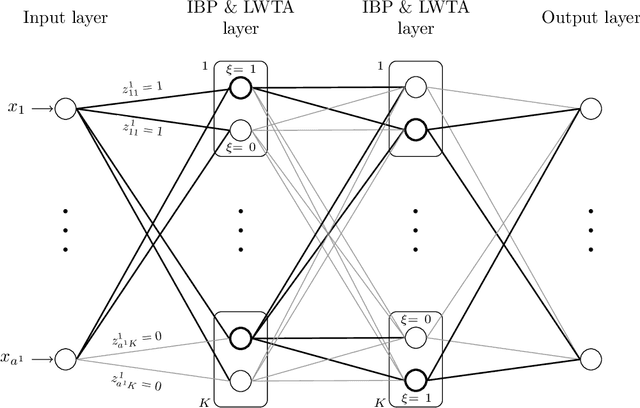
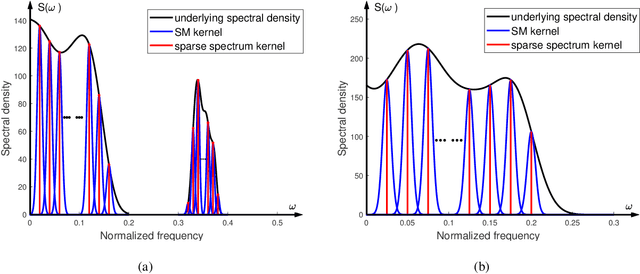
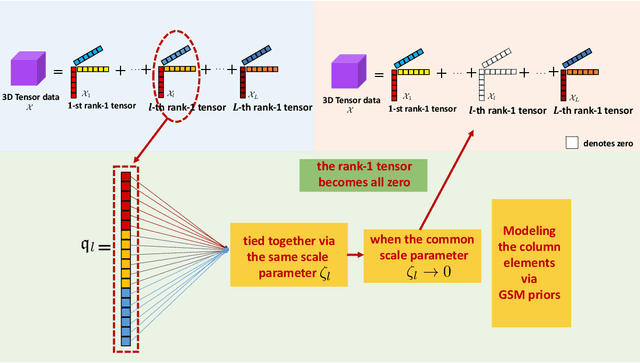
Sparse modeling for signal processing and machine learning has been at the focus of scientific research for over two decades. Among others, supervised sparsity-aware learning comprises two major paths paved by: a) discriminative methods and b) generative methods. The latter, more widely known as Bayesian methods, enable uncertainty evaluation w.r.t. the performed predictions. Furthermore, they can better exploit related prior information and naturally introduce robustness into the model, due to their unique capacity to marginalize out uncertainties related to the parameter estimates. Moreover, hyper-parameters associated with the adopted priors can be learnt via the training data. To implement sparsity-aware learning, the crucial point lies in the choice of the function regularizer for discriminative methods and the choice of the prior distribution for Bayesian learning. Over the last decade or so, due to the intense research on deep learning, emphasis has been put on discriminative techniques. However, a come back of Bayesian methods is taking place that sheds new light on the design of deep neural networks, which also establish firm links with Bayesian models and inspire new paths for unsupervised learning, such as Bayesian tensor decomposition. The goal of this article is two-fold. First, to review, in a unified way, some recent advances in incorporating sparsity-promoting priors into three highly popular data modeling tools, namely deep neural networks, Gaussian processes, and tensor decomposition. Second, to review their associated inference techniques from different aspects, including: evidence maximization via optimization and variational inference methods. Challenges such as small data dilemma, automatic model structure search, and natural prediction uncertainty evaluation are also discussed. Typical signal processing and machine learning tasks are demonstrated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge