ResNorm: Tackling Long-tailed Degree Distribution Issue in Graph Neural Networks via Normalization
Paper and Code
Jun 16, 2022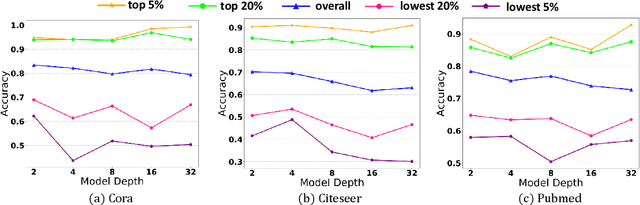
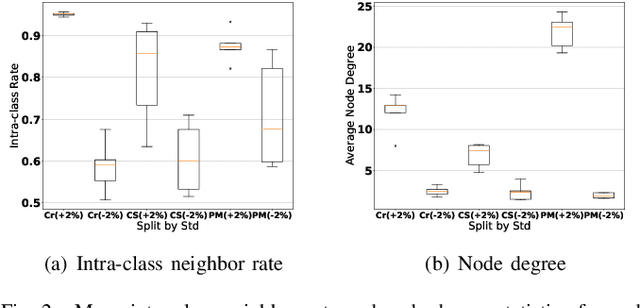
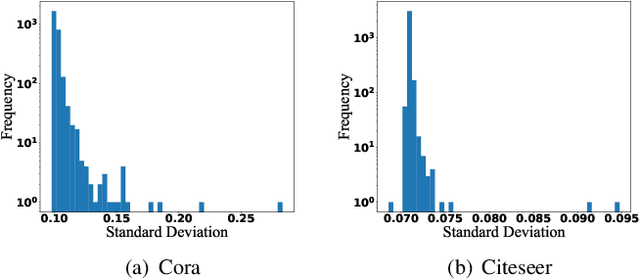
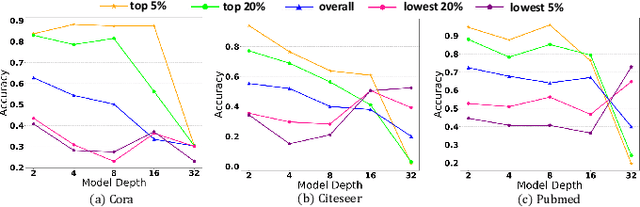
Graph Neural Networks (GNNs) have attracted much attention due to their ability in learning representations from graph-structured data. Despite the successful applications of GNNs in many domains, the optimization of GNNs is less well studied, and the performance on node classification heavily suffers from the long-tailed node degree distribution. This paper focuses on improving the performance of GNNs via normalization. In detail, by studying the long-tailed distribution of node degrees in the graph, we propose a novel normalization method for GNNs, which is termed ResNorm (\textbf{Res}haping the long-tailed distribution into a normal-like distribution via \textbf{norm}alization). The $scale$ operation of ResNorm reshapes the node-wise standard deviation (NStd) distribution so as to improve the accuracy of tail nodes (\textit{i}.\textit{e}., low-degree nodes). We provide a theoretical interpretation and empirical evidence for understanding the mechanism of the above $scale$. In addition to the long-tailed distribution issue, over-smoothing is also a fundamental issue plaguing the community. To this end, we analyze the behavior of the standard shift and prove that the standard shift serves as a preconditioner on the weight matrix, increasing the risk of over-smoothing. With the over-smoothing issue in mind, we design a $shift$ operation for ResNorm that simulates the degree-specific parameter strategy in a low-cost manner. Extensive experiments have validated the effectiveness of ResNorm on several node classification benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge