Resilient Active Information Gathering with Mobile Robots
Paper and Code
Sep 02, 2018
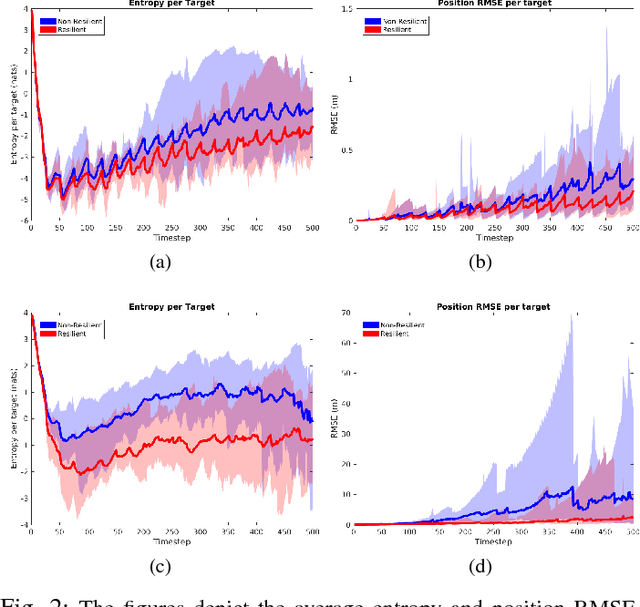

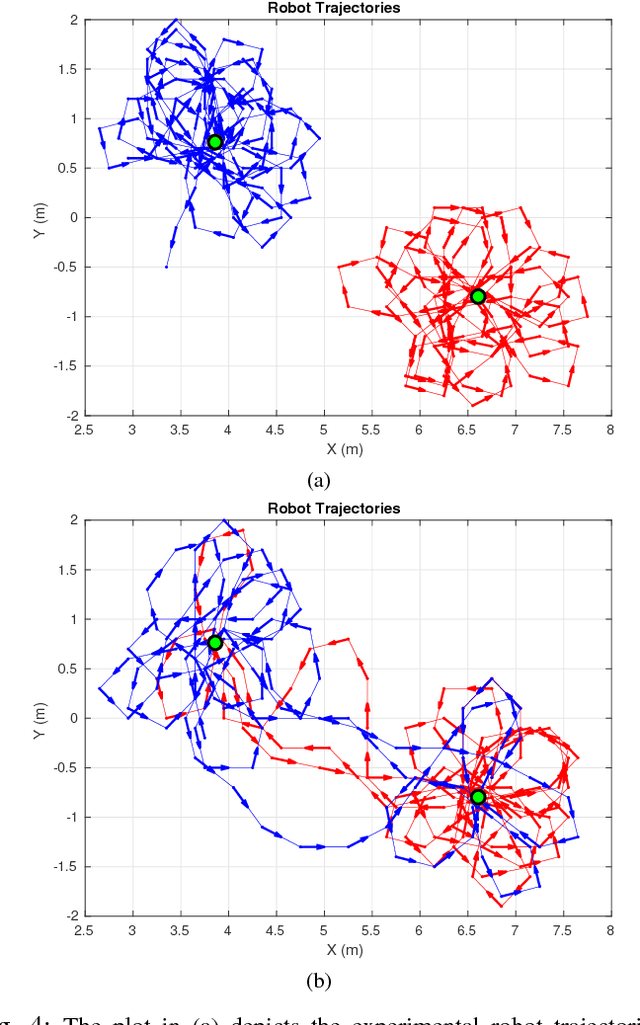
Applications of safety, security, and rescue in robotics, such as multi-robot target tracking, involve the execution of information acquisition tasks by teams of mobile robots. However, in failure-prone or adversarial environments, robots get attacked, their communication channels get jammed, and their sensors may fail, resulting in the withdrawal of robots from the collective task, and consequently the inability of the remaining active robots to coordinate with each other. As a result, traditional design paradigms become insufficient and, in contrast, resilient designs against system-wide failures and attacks become important. In general, resilient design problems are hard, and even though they often involve objective functions that are monotone or submodular, scalable approximation algorithms for their solution have been hitherto unknown. In this paper, we provide the first algorithm, enabling the following capabilities: minimal communication, i.e., the algorithm is executed by the robots based only on minimal communication between them; system-wide resiliency, i.e., the algorithm is valid for any number of denial-of-service attacks and failures; and provable approximation performance, i.e., the algorithm ensures for all monotone (and not necessarily submodular) objective functions a solution that is finitely close to the optimal. We quantify our algorithm's approximation performance using a notion of curvature for monotone set functions. We support our theoretical analyses with simulated and real-world experiments, by considering an active information gathering scenario, namely, multi-robot target tracking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge