Residual Expansion Algorithm: Fast and Effective Optimization for Nonconvex Least Squares Problems
Paper and Code
May 26, 2017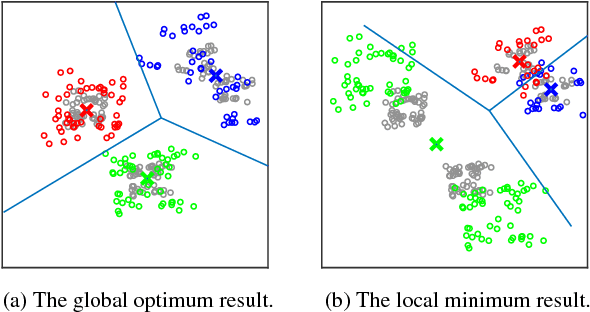

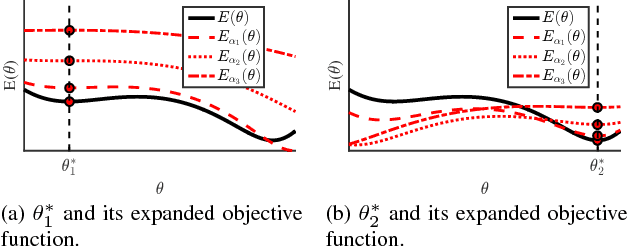
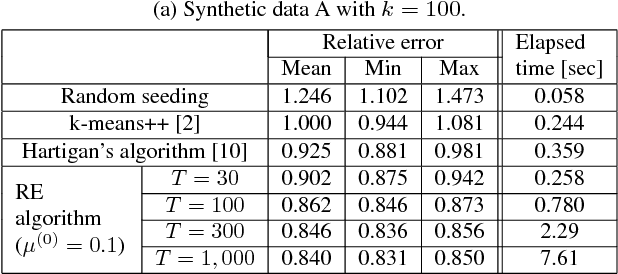
We propose the residual expansion (RE) algorithm: a global (or near-global) optimization method for nonconvex least squares problems. Unlike most existing nonconvex optimization techniques, the RE algorithm is not based on either stochastic or multi-point searches; therefore, it can achieve fast global optimization. Moreover, the RE algorithm is easy to implement and successful in high-dimensional optimization. The RE algorithm exhibits excellent empirical performance in terms of k-means clustering, point-set registration, optimized product quantization, and blind image deblurring.
* Accepted to CVPR2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge