Research on the inverse kinematics prediction of a soft actuator via BP neural network
Paper and Code
Oct 26, 2021


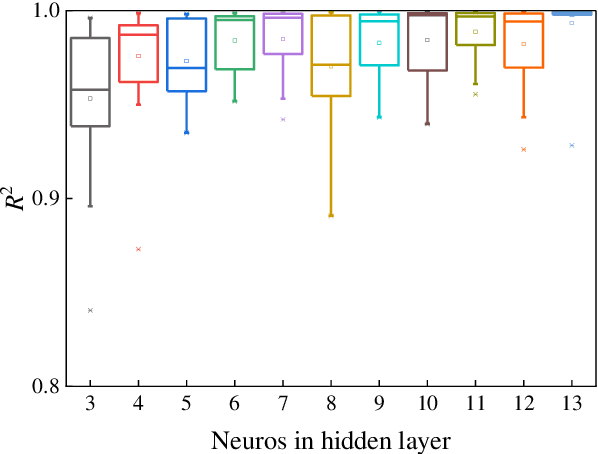
In this work we address the inverse kinetics problem of motion planning of the soft actuators driven by three chambers. Although the mathematical model describing inverse dynamics of this kind of actuator can been employed, this model is still a complex system. On the one hand, the differential equations are nonlinear, therefore, it is very difficult and time consuming to get the analytical solutions. Since the exact solutions of the mechanical model are not available, the elements of the Jacobian matrix cannot be calculated. On the other hand, material model is a complicated system with significant nonlinearity, non-stationarity, and uncertainty, making it challenging to develop an appropriate system model. To overcome these intrinsic problems, we propose a back-propagation (BP) neural network learning the inverse kinetics of the soft manipulator moving in three-dimensional space. After the training, the BP neural network model can represent the relation between the manipulator tip position and the pressures applied to the chambers. The proposed algorithm is very precise, and computationally efficient. The results show that a desired terminal position can be achieved with a degree of accuracy of 2.59% relative average error with respect to the total actuator length, demonstrate the ability of the model to realize inverse kinematic control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge