Reliable Estimation of Kullback-Leibler Divergence by Controlling Discriminator Complexity in the Reproducing Kernel Hilbert Space

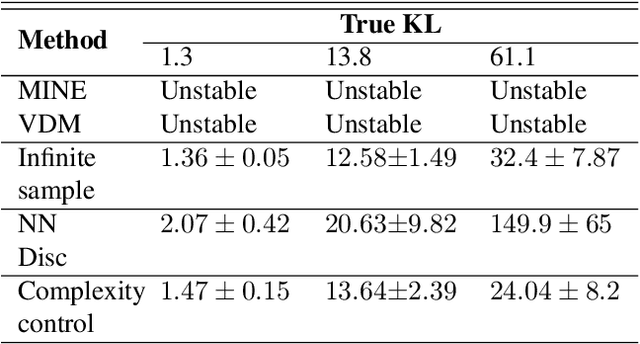
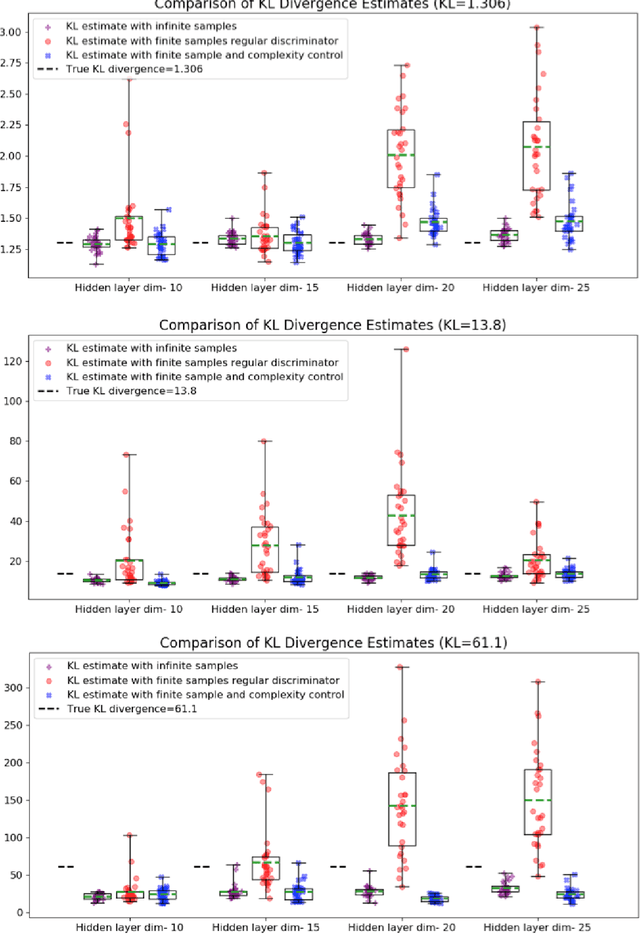
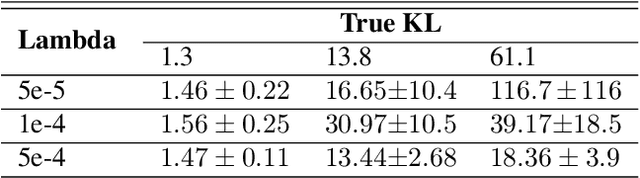
Several scalable methods to compute the Kullback Leibler (KL) divergence between two distributions using their samples have been proposed and applied in large-scale machine learning models. While they have been found to be unstable, the theoretical root cause of the problem is not clear. In this paper, we study in detail a generative adversarial network based approach that uses a neural network discriminator to estimate KL divergence. We argue that, in such case, high fluctuations in the estimates are a consequence of not controlling the complexity of the discriminator function space. We provide a theoretical underpinning and remedy for this problem through the following contributions. First, we construct a discriminator in the Reproducing Kernel Hilbert Space (RKHS). This enables us to leverage sample complexity and mean embedding to theoretically relate the error probability bound of the KL estimates to the complexity of the neural-net discriminator. Based on this theory, we then present a scalable way to control the complexity of the discriminator for a consistent estimation of KL divergence. We support both our proposed theory and method to control the complexity of the RKHS discriminator in controlled experiments.