Regularised Deep Reinforcement Learning with Guaranteed Convergence

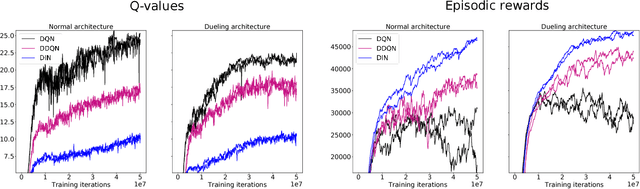
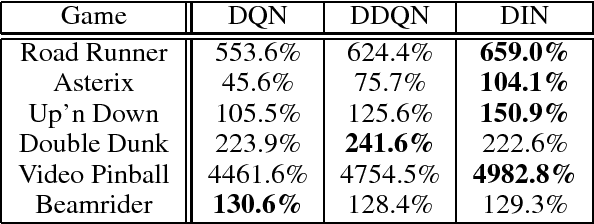
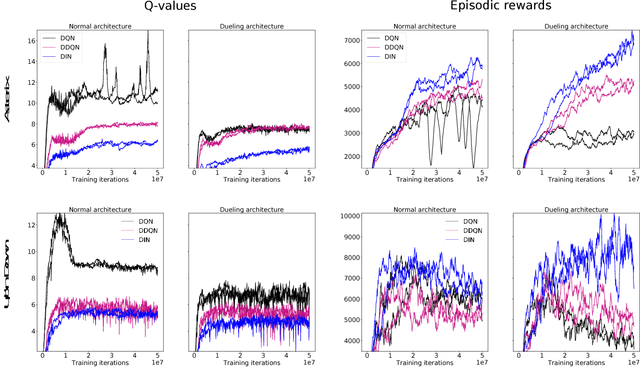
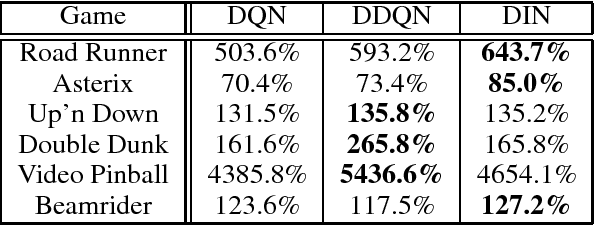
Deep Q-networks (DQNs) suffer from two important challenges hindering their application in real-world scenarios. First, DQNs overestimate Q-values which leads to increased sample complexity, and second, no theoretical convergence guarantees have been established. In this paper, we address both problems by introducing an intrinsic penalty signal arising from a Kullback-Leibler (KL) constraint that encourages reduced Q-value estimates. We then prove, for the first time, convergence to a stationary point under a specific scheduling of the penalisation magnitude. Our proofs operate in the deep reinforcement learning setting that considers convolutional and dense layers for Q-function approximation. Furthermore, we prove divergence of standard DQNs using a counter example that relates to the non-optimal choice of the history-scheduling parameter adopted by `vanilla' DQNs. We believe this can shed the light on some of the difficulties reported by researchers and practitioners in the field.