Regret Bounds for Gaussian-Process Optimization in Large Domains
Paper and Code
Apr 29, 2021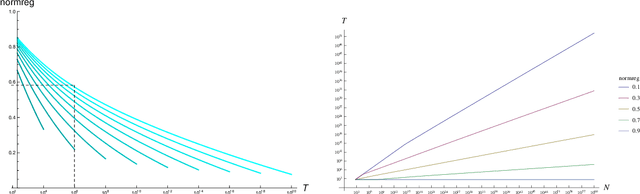
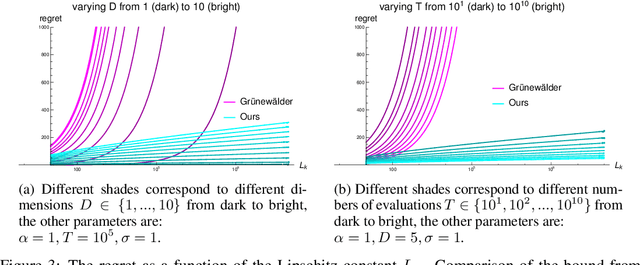
The goal of this paper is to characterize Gaussian-Process optimization in the setting where the function domain is large relative to the number of admissible function evaluations, i.e., where it is impossible to find the global optimum. We provide upper bounds on the suboptimality (Bayesian simple regret) of the solution found by optimization strategies that are closely related to the widely used expected improvement (EI) and upper confidence bound (UCB) algorithms. These regret bounds illuminate the relationship between the number of evaluations, the domain size (i.e. cardinality of finite domains / Lipschitz constant of the covariance function in continuous domains), and the optimality of the retrieved function value. In particular, they show that even when the number of evaluations is far too small to find the global optimum, we can find nontrivial function values (e.g. values that achieve a certain ratio with the optimal value).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge