Regret Analysis for Hierarchical Experts Bandit Problem
Paper and Code
Aug 11, 2022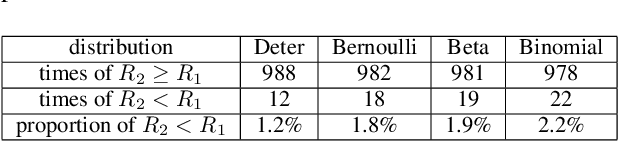

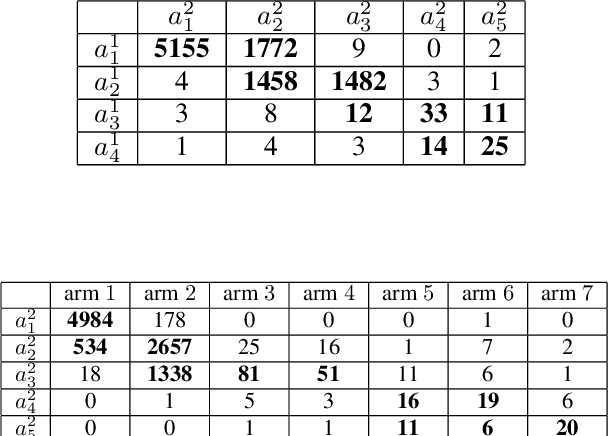

We study an extension of standard bandit problem in which there are R layers of experts. Multi-layered experts make selections layer by layer and only the experts in the last layer can play arms. The goal of the learning policy is to minimize the total regret in this hierarchical experts setting. We first analyze the case that total regret grows linearly with the number of layers. Then we focus on the case that all experts are playing Upper Confidence Bound (UCB) strategy and give several sub-linear upper bounds for different circumstances. Finally, we design some experiments to help the regret analysis for the general case of hierarchical UCB structure and show the practical significance of our theoretical results. This article gives many insights about reasonable hierarchical decision structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge