Refining neural network predictions using background knowledge
Paper and Code
Jun 10, 2022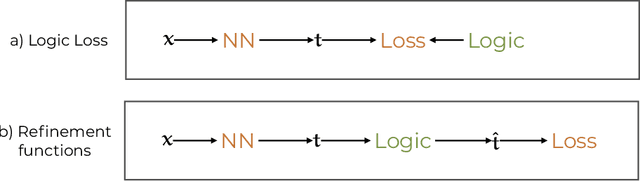
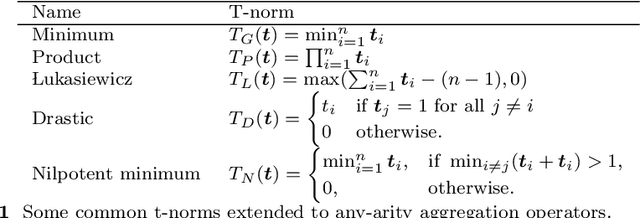
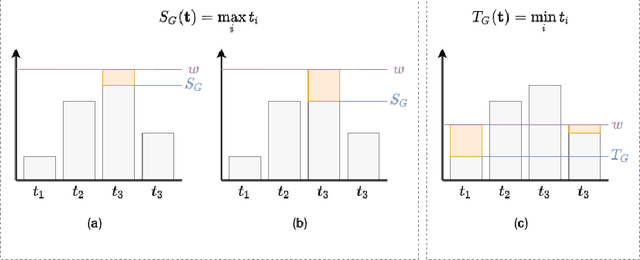
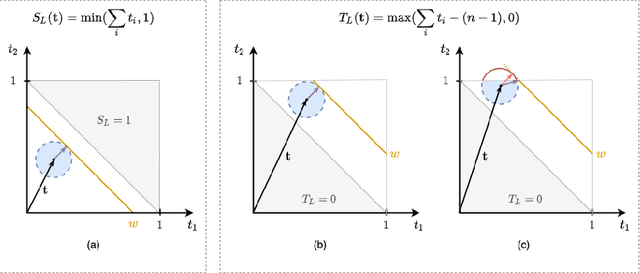
Recent work has showed we can use logical background knowledge in learning system to compensate for a lack of labeled training data. Many such methods work by creating a loss function that encodes this knowledge. However, often the logic is discarded after training, even if it is still useful at test-time. Instead, we ensure neural network predictions satisfy the knowledge by refining the predictions with an extra computation step. We introduce differentiable refinement functions that find a corrected prediction close to the original prediction. We study how to effectively and efficiently compute these refinement functions. Using a new algorithm, we combine refinement functions to find refined predictions for logical formulas of any complexity. This algorithm finds optimal refinements on complex SAT formulas in significantly fewer iterations and frequently finds solutions where gradient descent can not.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge