Redundancy of Hidden Layers in Deep Learning: An Information Perspective

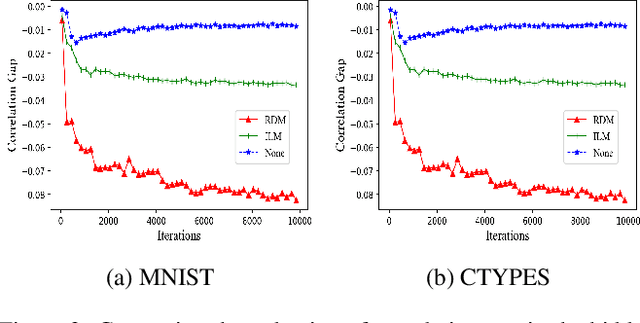
Although the deep structure guarantees the powerful expressivity of deep networks (DNNs), it also triggers serious overfitting problem. To improve the generalization capacity of DNNs, many strategies were developed to improve the diversity among hidden units. However, most of these strategies are empirical and heuristic in absence of either a theoretical derivation of the diversity measure or a clear connection from the diversity to the generalization capacity. In this paper, from an information theoretic perspective, we introduce a new definition of redundancy to describe the diversity of hidden units under supervised learning settings by formalizing the effect of hidden layers on the generalization capacity as the mutual information. We prove an opposite relationship existing between the defined redundancy and the generalization capacity, i.e., the decrease of redundancy generally improving the generalization capacity. The experiments show that the DNNs using the redundancy as the regularizer can effectively reduce the overfitting and decrease the generalization error, which well supports above points.