Recursive Importance Sketching for Rank Constrained Least Squares: Algorithms and High-order Convergence

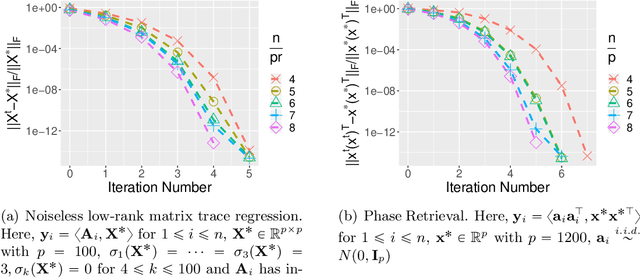
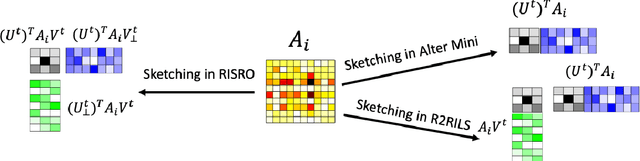
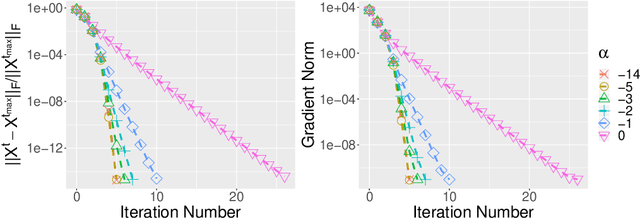
In this paper, we propose a new {\it \underline{R}ecursive} {\it \underline{I}mportance} {\it \underline{S}ketching} algorithm for {\it \underline{R}ank} constrained least squares {\it \underline{O}ptimization} (RISRO). As its name suggests, the algorithm is based on a new sketching framework, recursive importance sketching. Several existing algorithms in the literature can be reinterpreted under the new sketching framework and RISRO offers clear advantages over them. RISRO is easy to implement and computationally efficient, where the core procedure in each iteration is only solving a dimension reduced least squares problem. Different from numerous existing algorithms with locally geometric convergence rate, we establish the local quadratic-linear and quadratic rate of convergence for RISRO under some mild conditions. In addition, we discover a deep connection of RISRO to Riemannian manifold optimization on fixed rank matrices. The effectiveness of RISRO is demonstrated in two applications in machine learning and statistics: low-rank matrix trace regression and phase retrieval. Simulation studies demonstrate the superior numerical performance of RISRO.