Rate-Constrained Remote Contextual Bandits
Paper and Code
Apr 26, 2022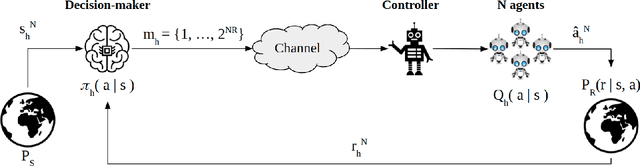
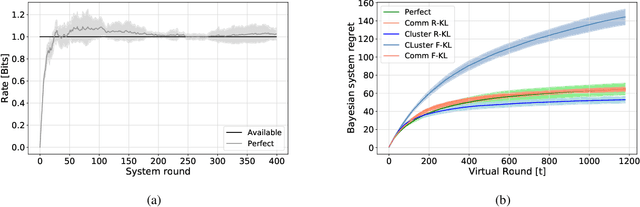
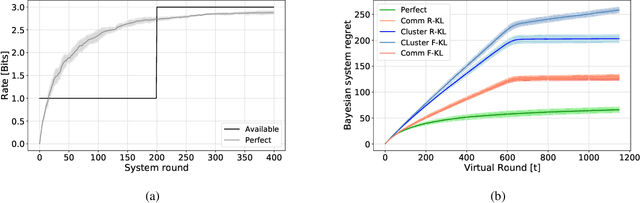
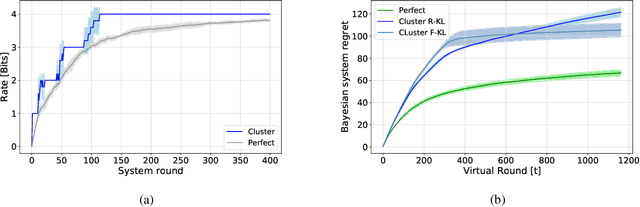
We consider a rate-constrained contextual multi-armed bandit (RC-CMAB) problem, in which a group of agents are solving the same contextual multi-armed bandit (CMAB) problem. However, the contexts are observed by a remotely connected entity, i.e., the decision-maker, that updates the policy to maximize the returned rewards, and communicates the arms to be sampled by the agents to a controller over a rate-limited communications channel. This framework can be applied to personalized ad placement, whenever the content owner observes the website visitors, and hence has the context, but needs to transmit the ads to be shown to a controller that is in charge of placing the marketing content. Consequently, the rate-constrained CMAB (RC-CMAB) problem requires the study of lossy compression schemes for the policy to be employed whenever the constraint on the channel rate does not allow the uncompressed transmission of the decision-maker's intentions. We characterize the fundamental information theoretic limits of this problem by letting the number of agents go to infinity, and study the regret that can be achieved, identifying the two distinct rate regions leading to linear and sub-linear regrets respectively. We then analyze the optimal compression scheme achievable in the limit with infinite agents, when using the forward and reverse KL divergence as distortion metric. Based on this, we also propose a practical coding scheme, and provide numerical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge