RAT iLQR: A Risk Auto-Tuning Controller to Optimally Account for Stochastic Model Mismatch
Paper and Code
Oct 16, 2020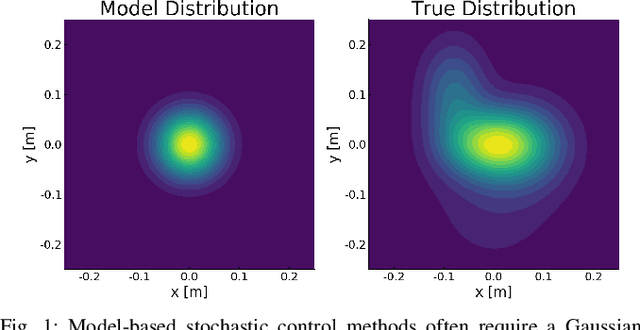
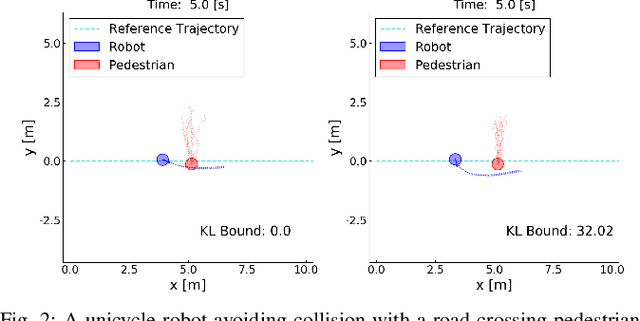
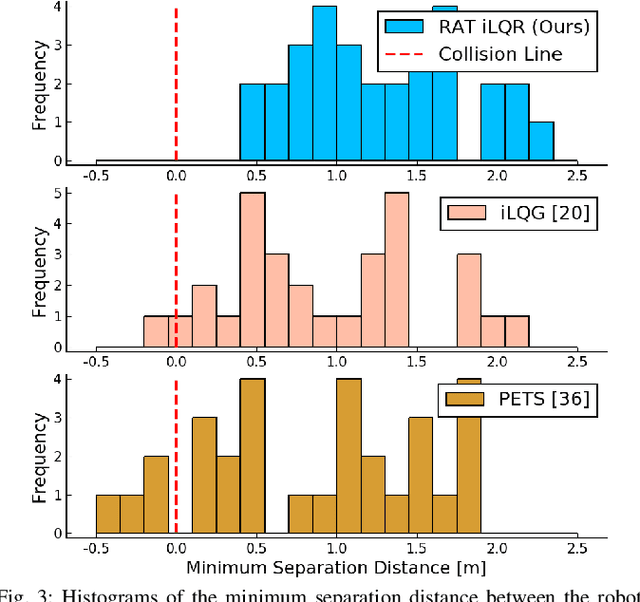
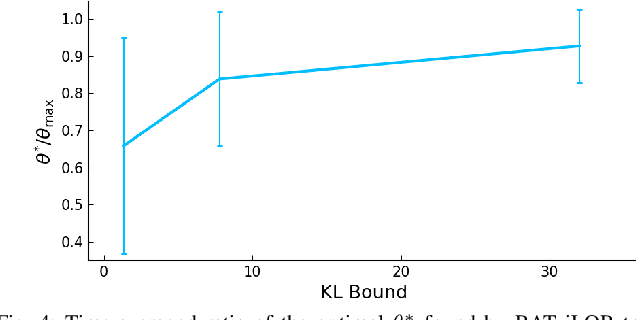
Successful robotic operation in stochastic environments relies on accurate characterization of the underlying probability distributions, yet this is often imperfect due to limited knowledge. This work presents a control algorithm that is capable of handling such distributional mismatches. Specifically, we propose a novel nonlinear MPC for distributionally robust control, which plans locally optimal feedback policies against a worst-case distribution within a given KL divergence bound from a Gaussian distribution. Leveraging mathematical equivalence between distributionally robust control and risk-sensitive optimal control, our framework also provides an algorithm to dynamically adjust the risk-sensitivity level online for risk-sensitive control. The benefits of the distributional robustness as well as the automatic risk-sensitivity adjustment are demonstrated in a dynamic collision avoidance scenario where the predictive distribution of human motion is erroneous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge