Random Maxout Features
Paper and Code
Jun 12, 2015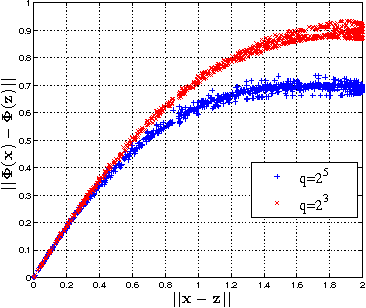

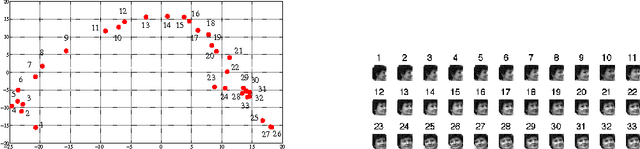

In this paper, we propose and study random maxout features, which are constructed by first projecting the input data onto sets of randomly generated vectors with Gaussian elements, and then outputing the maximum projection value for each set. We show that the resulting random feature map, when used in conjunction with linear models, allows for the locally linear estimation of the function of interest in classification tasks, and for the locally linear embedding of points when used for dimensionality reduction or data visualization. We derive generalization bounds for learning that assess the error in approximating locally linear functions by linear functions in the maxout feature space, and empirically evaluate the efficacy of the approach on the MNIST and TIMIT classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge