Quantum Inspired Training for Boltzmann Machines
Paper and Code
Jul 09, 2015
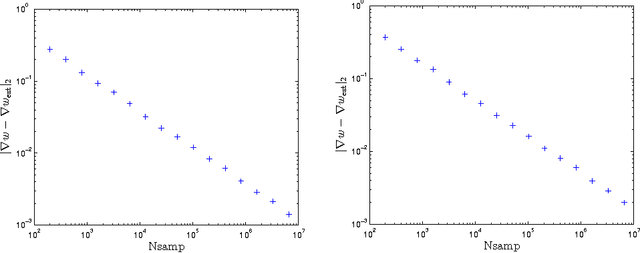

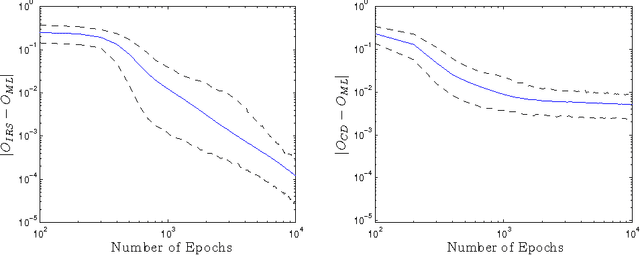
We present an efficient classical algorithm for training deep Boltzmann machines (DBMs) that uses rejection sampling in concert with variational approximations to estimate the gradients of the training objective function. Our algorithm is inspired by a recent quantum algorithm for training DBMs. We obtain rigorous bounds on the errors in the approximate gradients; in turn, we find that choosing the instrumental distribution to minimize the alpha=2 divergence with the Gibbs state minimizes the asymptotic algorithmic complexity. Our rejection sampling approach can yield more accurate gradients than low-order contrastive divergence training and the costs incurred in finding increasingly accurate gradients can be easily parallelized. Finally our algorithm can train full Boltzmann machines and scales more favorably with the number of layers in a DBM than greedy contrastive divergence training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge