Q-FIT: The Quantifiable Feature Importance Technique for Explainable Machine Learning

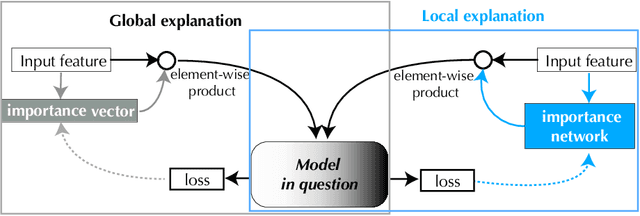
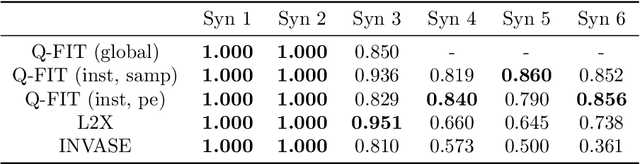
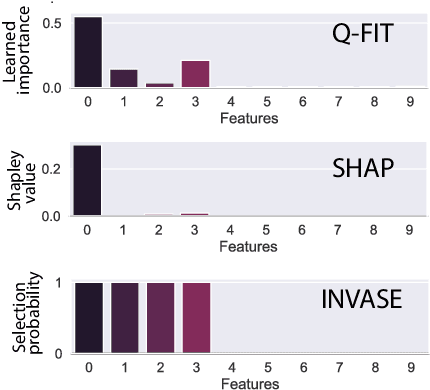
We introduce a novel framework to quantify the importance of each input feature for model explainability. A user of our framework can choose between two modes: (a) global explanation: providing feature importance globally across all the data points; and (b) local explanation: providing feature importance locally for each individual data point. The core idea of our method comes from utilizing the Dirichlet distribution to define a distribution over the importance of input features. This particular distribution is useful in ranking the importance of the input features as a sample from this distribution is a probability vector (i.e., the vector components sum to 1), Thus, the ranking uncovered by our framework which provides a \textit{quantifiable explanation} of how significant each input feature is to a model's output. This quantifiable explainability differentiates our method from existing feature-selection methods, which simply determine whether a feature is relevant or not. Furthermore, a distribution over the explanation allows to define a closed-form divergence to measure the similarity between learned feature importance under different models. We use this divergence to study how the feature importance trade-offs with essential notions in modern machine learning, such as privacy and fairness. We show the effectiveness of our method on a variety of synthetic and real datasets, taking into account both tabular and image datasets.