Pure Exploration in Infinitely-Armed Bandit Models with Fixed-Confidence
Paper and Code
Mar 13, 2018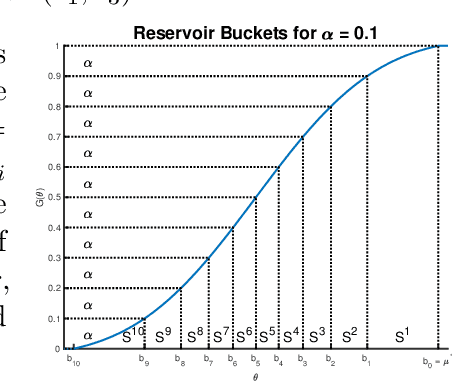
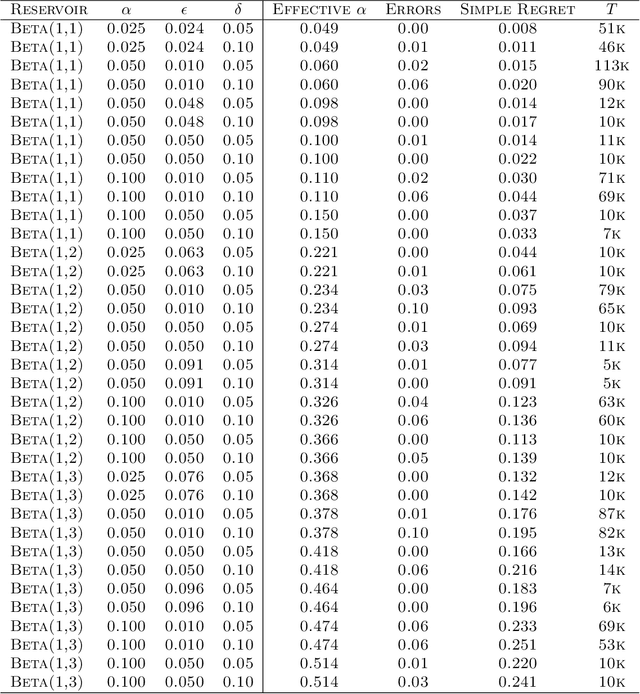
We consider the problem of near-optimal arm identification in the fixed confidence setting of the infinitely armed bandit problem when nothing is known about the arm reservoir distribution. We (1) introduce a PAC-like framework within which to derive and cast results; (2) derive a sample complexity lower bound for near-optimal arm identification; (3) propose an algorithm that identifies a nearly-optimal arm with high probability and derive an upper bound on its sample complexity which is within a log factor of our lower bound; and (4) discuss whether our log^2(1/delta) dependence is inescapable for "two-phase" (select arms first, identify the best later) algorithms in the infinite setting. This work permits the application of bandit models to a broader class of problems where fewer assumptions hold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge