Pull Message Passing for Nonparametric Belief Propagation
Paper and Code
Jul 27, 2018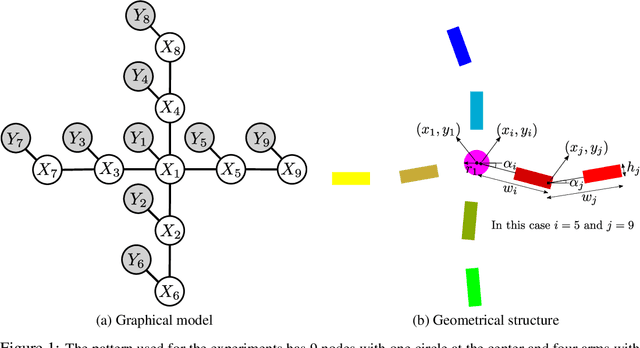

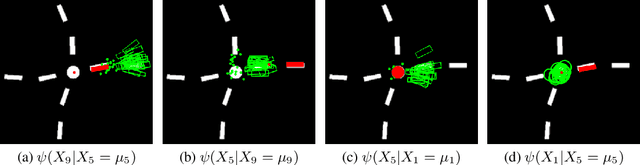

We present a "pull" approach to approximate products of Gaussian mixtures within message updates for Nonparametric Belief Propagation (NBP) inference. Existing NBP methods often represent messages between continuous-valued latent variables as Gaussian mixture models. To avoid computational intractability in loopy graphs, NBP necessitates an approximation of the product of such mixtures. Sampling-based product approximations have shown effectiveness for NBP inference. However, such approximations used within the traditional "push" message update procedures quickly become computationally prohibitive for multi-modal distributions over high-dimensional variables. In contrast, we propose a "pull" method, as the Pull Message Passing for Nonparametric Belief propagation (PMPNBP) algorithm, and demonstrate its viability for efficient inference. We report results using an experiment from an existing NBP method, PAMPAS, for inferring the pose of an articulated structure in clutter. Results from this illustrative problem found PMPNBP has a greater ability to efficiently scale the number of components in its mixtures and, consequently, improve inference accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge