Provably Efficient Multi-Agent Reinforcement Learning with Fully Decentralized Communication
Paper and Code
Oct 14, 2021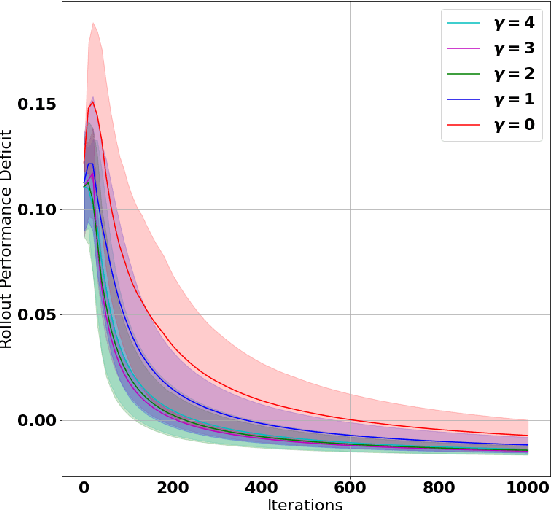
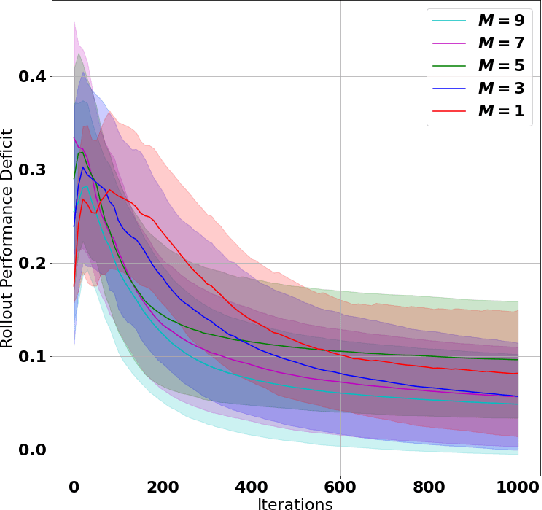
A challenge in reinforcement learning (RL) is minimizing the cost of sampling associated with exploration. Distributed exploration reduces sampling complexity in multi-agent RL (MARL). We investigate the benefits to performance in MARL when exploration is fully decentralized. Specifically, we consider a class of online, episodic, tabular $Q$-learning problems under time-varying reward and transition dynamics, in which agents can communicate in a decentralized manner.We show that group performance, as measured by the bound on regret, can be significantly improved through communication when each agent uses a decentralized message-passing protocol, even when limited to sending information up to its $\gamma$-hop neighbors. We prove regret and sample complexity bounds that depend on the number of agents, communication network structure and $\gamma.$ We show that incorporating more agents and more information sharing into the group learning scheme speeds up convergence to the optimal policy. Numerical simulations illustrate our results and validate our theoretical claims.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge