Provably Correct Optimization and Exploration with Non-linear Policies
Paper and Code
Mar 22, 2021

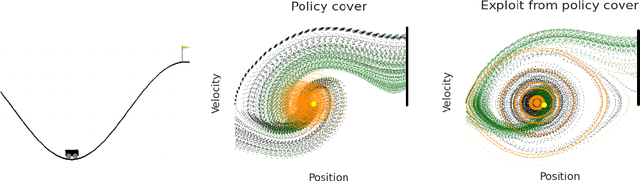
Policy optimization methods remain a powerful workhorse in empirical Reinforcement Learning (RL), with a focus on neural policies that can easily reason over complex and continuous state and/or action spaces. Theoretical understanding of strategic exploration in policy-based methods with non-linear function approximation, however, is largely missing. In this paper, we address this question by designing ENIAC, an actor-critic method that allows non-linear function approximation in the critic. We show that under certain assumptions, e.g., a bounded eluder dimension $d$ for the critic class, the learner finds a near-optimal policy in $O(\poly(d))$ exploration rounds. The method is robust to model misspecification and strictly extends existing works on linear function approximation. We also develop some computational optimizations of our approach with slightly worse statistical guarantees and an empirical adaptation building on existing deep RL tools. We empirically evaluate this adaptation and show that it outperforms prior heuristics inspired by linear methods, establishing the value via correctly reasoning about the agent's uncertainty under non-linear function approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge