Provable More Data Hurt in High Dimensional Least Squares Estimator

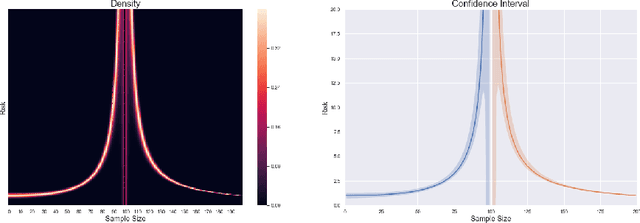
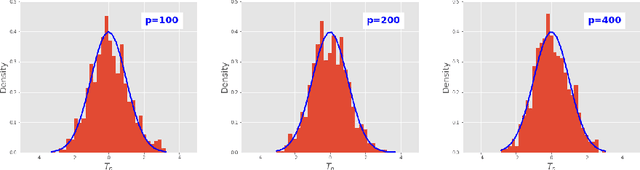
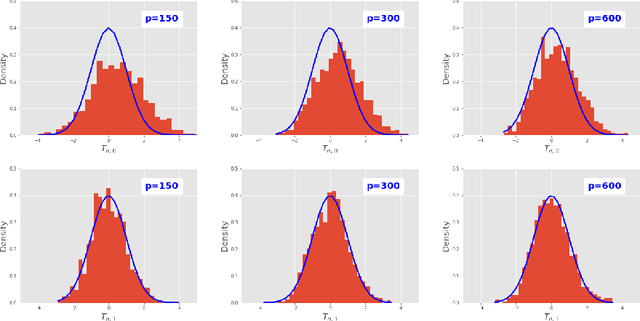
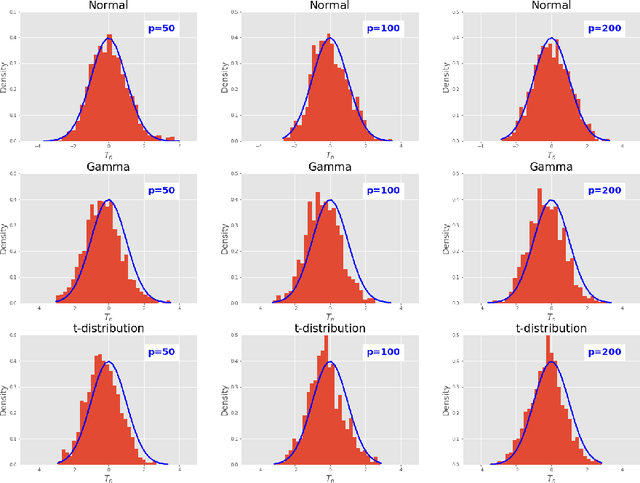
This paper investigates the finite-sample prediction risk of the high-dimensional least squares estimator. We derive the central limit theorem for the prediction risk when both the sample size and the number of features tend to infinity. Furthermore, the finite-sample distribution and the confidence interval of the prediction risk are provided. Our theoretical results demonstrate the sample-wise nonmonotonicity of the prediction risk and confirm "more data hurt" phenomenon.