Proportional Aggregation of Preferences for Sequential Decision Making
Paper and Code
Jun 26, 2023
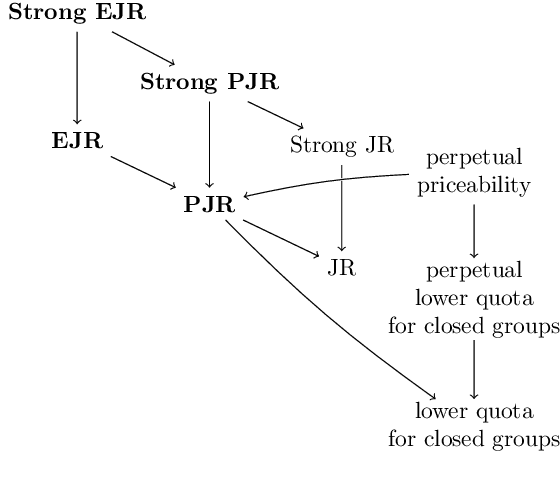
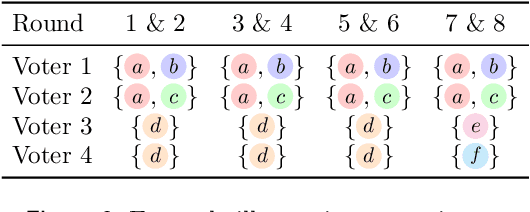
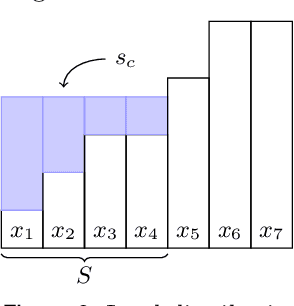
We study the problem of fair sequential decision making given voter preferences. In each round, a decision rule must choose a decision from a set of alternatives where each voter reports which of these alternatives they approve. Instead of going with the most popular choice in each round, we aim for proportional representation. We formalize this aim using axioms based on Proportional Justified Representation (PJR), which were proposed in the literature on multi-winner voting and were recently adapted to multi-issue decision making. The axioms require that every group of $\alpha\%$ of the voters, if it agrees in every round (i.e., approves a common alternative), then those voters must approve at least $\alpha\%$ of the decisions. A stronger version of the axioms requires that every group of $\alpha\%$ of the voters that agrees in a $\beta$ fraction of rounds must approve $\beta\cdot\alpha\%$ of the decisions. We show that three attractive voting rules satisfy axioms of this style. One of them (Sequential Phragm\'en) makes its decisions online, and the other two satisfy strengthened versions of the axioms but make decisions semi-online (Method of Equal Shares) or fully offline (Proportional Approval Voting). The first two are polynomial-time computable, and the latter is based on an NP-hard optimization, but it admits a polynomial-time local search algorithm that satisfies the same axiomatic properties. We present empirical results about the performance of these rules based on synthetic data and U.S. political elections. We also run experiments where votes are cast by preference models trained on user responses from the moral machine dataset about ethical dilemmas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge