Proper Value Equivalence

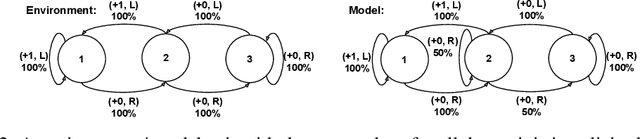
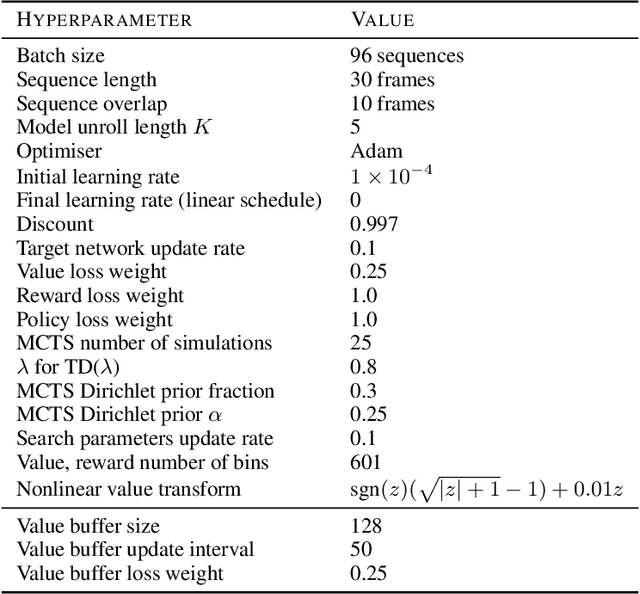
One of the main challenges in model-based reinforcement learning (RL) is to decide which aspects of the environment should be modeled. The value-equivalence (VE) principle proposes a simple answer to this question: a model should capture the aspects of the environment that are relevant for value-based planning. Technically, VE distinguishes models based on a set of policies and a set of functions: a model is said to be VE to the environment if the Bellman operators it induces for the policies yield the correct result when applied to the functions. As the number of policies and functions increase, the set of VE models shrinks, eventually collapsing to a single point corresponding to a perfect model. A fundamental question underlying the VE principle is thus how to select the smallest sets of policies and functions that are sufficient for planning. In this paper we take an important step towards answering this question. We start by generalizing the concept of VE to order-$k$ counterparts defined with respect to $k$ applications of the Bellman operator. This leads to a family of VE classes that increase in size as $k \rightarrow \infty$. In the limit, all functions become value functions, and we have a special instantiation of VE which we call proper VE or simply PVE. Unlike VE, the PVE class may contain multiple models even in the limit when all value functions are used. Crucially, all these models are sufficient for planning, meaning that they will yield an optimal policy despite the fact that they may ignore many aspects of the environment. We construct a loss function for learning PVE models and argue that popular algorithms such as MuZero and Muesli can be understood as minimizing an upper bound for this loss. We leverage this connection to propose a modification to MuZero and show that it can lead to improved performance in practice.