Projection techniques to update the truncated SVD of evolving matrices
Paper and Code
Oct 13, 2020
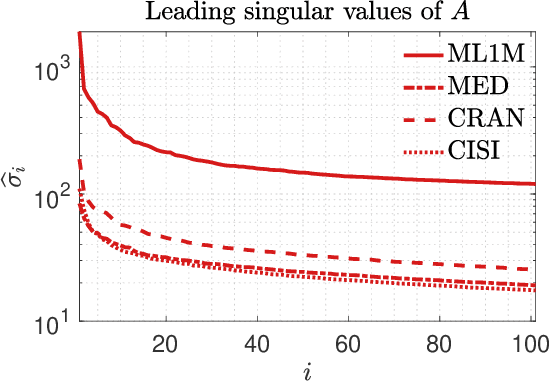
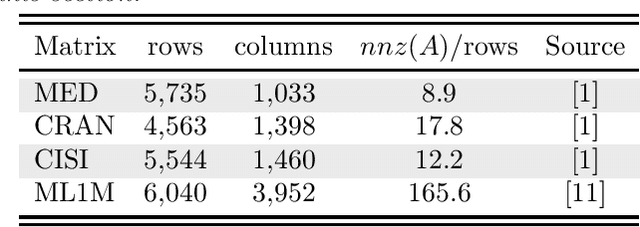
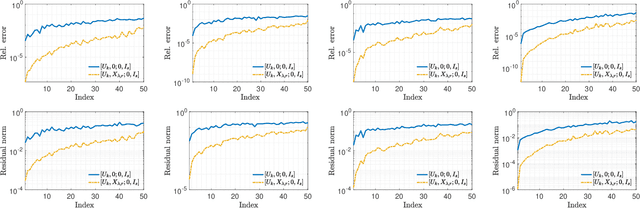
This paper considers the problem of updating the rank-k truncated Singular Value Decomposition (SVD) of matrices subject to the addition of new rows and/or columns over time. Such matrix problems represent an important computational kernel in applications such as Latent Semantic Indexing and Recommender Systems. Nonetheless, the proposed framework is purely algebraic and targets general updating problems. The algorithm presented in this paper undertakes a projection view-point and focuses on building a pair of subspaces which approximate the linear span of the sought singular vectors of the updated matrix. We discuss and analyze two different choices to form the projection subspaces. Results on matrices from real applications suggest that the proposed algorithm can lead to higher accuracy, especially for the singular triplets associated with the largest modulus singular values. Several practical details and key differences with other approaches are also discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge