Projection-Based Constrained Policy Optimization
Paper and Code
Oct 07, 2020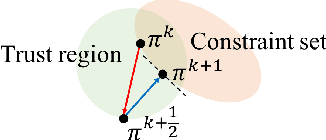
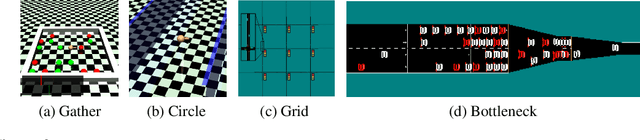
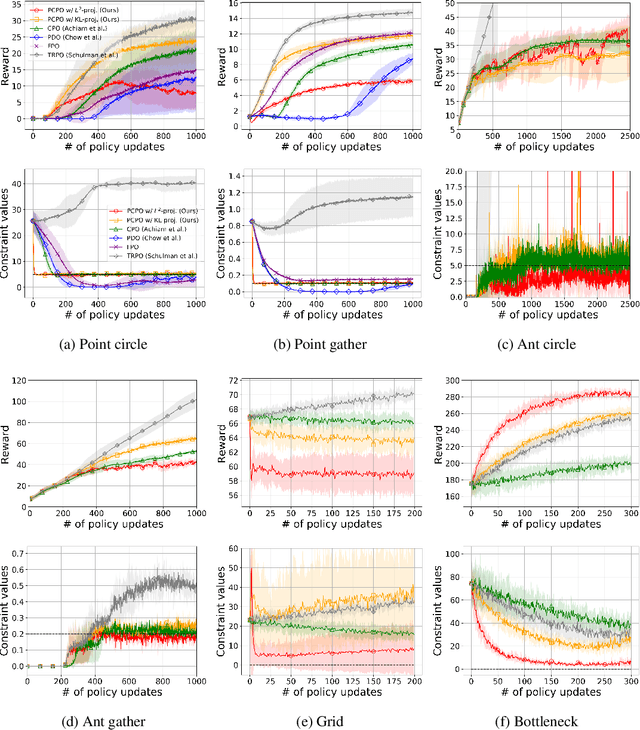
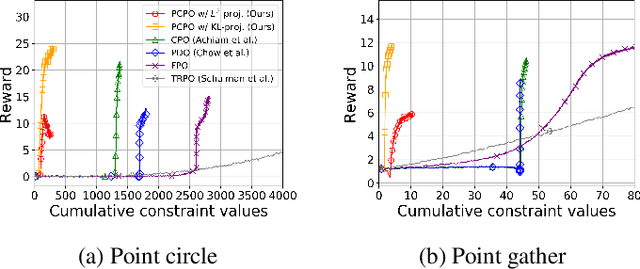
We consider the problem of learning control policies that optimize a reward function while satisfying constraints due to considerations of safety, fairness, or other costs. We propose a new algorithm, Projection-Based Constrained Policy Optimization (PCPO). This is an iterative method for optimizing policies in a two-step process: the first step performs a local reward improvement update, while the second step reconciles any constraint violation by projecting the policy back onto the constraint set. We theoretically analyze PCPO and provide a lower bound on reward improvement, and an upper bound on constraint violation, for each policy update. We further characterize the convergence of PCPO based on two different metrics: $\normltwo$ norm and Kullback-Leibler divergence. Our empirical results over several control tasks demonstrate that PCPO achieves superior performance, averaging more than 3.5 times less constraint violation and around 15\% higher reward compared to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge